RD Sharma Solutions for Class 10 Maths Chapter 5 Trigonometric Ratios
RD Sharma Solutions for Class 10 Maths Chapter 5 Exercise 5.1 Page No: 5.23
1. In each of the following, one of the six trigonometric ratios s given. Find the values of the other trigonometric ratios.

(i) sin A = 2/3
Solution:
We have,
sin A = 2/3 ……..….. (1)
As we know, by sin definition;
sin A = Perpendicular/ Hypotenuse = 2/3 ….(2)
By comparing eq. (1) and (2), we have
Opposite side = 2 and Hypotenuse = 3
Now, on using Pythagoras theorem in Δ ABC
AC2 = AB2 + BC2
Putting the values of perpendicular side (BC) and hypotenuse (AC) and for the base side as (AB), we get
⇒ 32 = AB2 + 22
AB2 = 32 – 22
AB2 = 9 – 4
AB2 = 5
AB = √5
Hence, Base = √5
By definition,
cos A = Base/Hypotenuse
⇒ cos A = √5/3
Since, cosec A = 1/sin A = Hypotenuse/Perpendicular
⇒ cosec A = 3/2
And, sec A = Hypotenuse/Base
⇒ sec A = 3/√5
And, tan A = Perpendicular/Base
⇒ tan A = 2/√5
And, cot A = 1/ tan A = Base/Perpendicular
⇒ cot A = √5/2
(ii) cos A = 4/5
Solution:
We have,
cos A = 4/5 …….…. (1)
As we know, by cos defination
cos A = Base/Hypotenuse …. (2)
By comparing eq. (1) and (2), we get
Base = 4 and Hypotenuse = 5
Now, using Pythagoras theorem in Δ ABC
AC2 = AB2 + BC2
Putting the value of base (AB) and hypotenuse (AC) and for the perpendicular (BC), we get
52 = 42 + BC2
BC2 = 52 – 42
BC2 = 25 – 16
BC2 = 9
BC= 3
Hence, Perpendicular = 3
By definition,
sin A = Perpendicular/Hypotenuse
⇒ sin A = 3/5
Then, cosec A = 1/sin A
⇒ cosec A= 1/ (3/5) = 5/3 = Hypotenuse/Perependicular
And, sec A = 1/cos A
⇒ sec A =Hypotenuse/Base
sec A = 5/4
And, tan A = Perpendicular/Base
⇒ tan A = 3/4
Next, cot A = 1/tan A = Base/Perpendicular
∴ cot A = 4/3
(iii) tan θ = 11/1
Solution:
We have, tan θ = 11…..…. (1)
By definition,
tan θ = Perpendicular/ Base…. (2)
On Comparing eq. (1) and (2), we get;
Base = 1 and Perpendicular = 5
Now, using Pythagoras theorem in Δ ABC.
AC2 = AB2 + BC2
Putting the value of base (AB) and perpendicular (BC) to get hypotenuse(AC), we get;
AC2 = 12 + 112
AC2 = 1 + 121
AC2= 122
AC= √122
Hence, hypotenuse = √122
By definition,
sin = Perpendicular/Hypotenuse
⇒ sin θ = 11/√122
And, cosec θ = 1/sin θ
⇒ cosec θ = √122/11
Next, cos θ = Base/ Hypotenuse
⇒ cos θ = 1/√122
And, sec θ = 1/cos θ
⇒ sec θ = √122/1 = √122
And, cot θ = 1/tan θ
∴ cot θ = 1/11
(iv) sin θ = 11/15
Solution:
We have, sin θ = 11/15 ………. (1)
By definition,
sin θ = Perpendicular/ Hypotenuse …. (2)
On Comparing eq. (1) and (2), we get;
Perpendicular = 11 and Hypotenuse= 15
Now, using Pythagoras theorem in Δ ABC
AC2 = AB2 + BC2
Putting the value of perpendicular (BC) and hypotenuse (AC) to get the base (AB), we have
152 = AB2 +112
AB2 = 152 – 112
AB2 = 225 – 121
AB2 = 104
AB = √104
AB= √ (2×2×2×13)
AB= 2√(2×13)
AB= 2√26
Hence, Base = 2√26
By definition,
cos θ = Base/Hypotenuse
∴ cosθ = 2√26/ 15
And, cosec θ = 1/sin θ
∴ cosec θ = 15/11
And, secθ = Hypotenuse/Base
∴ secθ =15/ 2√26
And, tan θ = Perpendicular/Base
∴ tanθ =11/ 2√26
And, cot θ = Base/Perpendicular
∴ cotθ =2√26/ 11
(v) tan α = 5/12
Solution:
We have, tan α = 5/12 …. (1)
By definition,
tan α = Perpendicular/Base…. (2)
On Comparing eq. (1) and (2), we get
Base = 12 and Perpendicular side = 5
Now, using Pythagoras theorem in Δ ABC
AC2 = AB2 + BC2
Putting the value of base (AB) and the perpendicular (BC) to get hypotenuse (AC), we have
AC2 = 122 + 52
AC2 = 144 + 25
AC2= 169
AC = 13 [After taking sq root on both sides]
Hence, Hypotenuse = 13
By definition,
sin α = Perpendicular/Hypotenuse
∴ sin α = 5/13
And, cosec α = Hypotenuse/Perpendicular
∴ cosec α = 13/5
And, cos α = Base/Hypotenuse
∴ cos α = 12/13
And, sec α =1/cos α
∴ sec α = 13/12
And, tan α = sin α/cos α
∴ tan α=5/12
Since, cot α = 1/tan α
∴ cot α =12/5
(vi) sin θ = √3/2
Solution:
We have, sin θ = √3/2 …………. (1)
By definition,
sin θ = Perpendicular/ Hypotenuse….(2)
On Comparing eq. (1) and (2), we get;
Perpendicular = √3 and Hypotenuse = 2
Now, using Pythagoras theorem in Δ ABC
AC2 = AB2 + BC2
Putting the value of perpendicular (BC) and hypotenuse (AC) and get the base (AB), we get;
22 = AB2 + (√3)2
AB2 = 22 – (√3)2
AB2 = 4 – 3
AB2 = 1
AB = 1
Thus, Base = 1
By definition,
cos θ = Base/Hypotenuse
∴ cos θ = 1/2
And, cosec θ = 1/sin θ
Or cosec θ= Hypotenuse/Perpendicualar
∴ cosec θ =2/√3
And, sec θ = Hypotenuse/Base
∴ sec θ = 2/1
And, tan θ = Perpendicula/Base
∴ tan θ = √3/1
And, cot θ = Base/Perpendicular
∴ cot θ = 1/√3
(vii) cos θ = 7/25
Solution:
We have, cos θ = 7/25 ……….. (1)
By definition,
cos θ = Base/Hypotenuse
On Comparing eq. (1) and (2), we get;
Base = 7 and Hypotenuse = 25
Now, using Pythagoras theorem in Δ ABC
AC2= AB2 + BC2
Putting the value of base (AB) and hypotenuse (AC) to get the perpendicular (BC)
252 = 72 +BC2
BC2 = 252 – 72
BC2 = 625 – 49
BC2 = 576
BC= √576
BC= 24
Hence, Perpendicular side = 24
By definition,
sin θ = perpendicular/Hypotenuse
∴ sin θ = 24/25
Since, cosec θ = 1/sin θ
Also, cosec θ= Hypotenuse/Perpendicualar
∴ cosec θ = 25/24
Since, sec θ = 1/cosec θ
Also, sec θ = Hypotenuse/Base
∴ sec θ = 25/7
Since, tan θ = Perpendicular/Base
∴ tan θ = 24/7
Now, cot = 1/tan θ
So, cot θ = Base/Perpendicular
∴ cot θ = 7/24
(viii) tan θ = 8/15
Solution:
We have, tan θ = 8/15 …………. (1)
By definition,
tan θ = Perpendicular/Base …. (2)
On Comparing eq. (1) and (2), we get;
Base = 15 and Perpendicular = 8
Now, using Pythagoras theorem in Δ ABC
AC2 = 152 + 82
AC2 = 225 + 64
AC2 = 289
AC = √289
AC = 17
Hence, Hypotenuse = 17
By definition,
Since, sin θ = perpendicular/Hypotenuse
∴ sin θ = 8/17
Since, cosec θ = 1/sin θ
Also, cosec θ = Hypotenuse/Perpendicualar
∴ cosec θ = 17/8
Since, cos θ = Base/Hypotenuse
∴ cos θ = 15/17
Since, sec θ = 1/cos θ
Also, sec θ = Hypotenuse/Base
∴ sec θ = 17/15
Since, cot θ = 1/tan θ
Also, cot θ = Base/Perpendicular
∴ cot θ = 15/8
(ix) cot θ = 12/5
Solution:
We have, cot θ = 12/5 …………. (1)
By definition,
cot θ = 1/tan θ
cot θ = Base/Perpendicular ……. (2)
On Comparing eq. (1) and (2), we have
Base = 12 and Perpendicular side = 5
Now, using Pythagoras theorem in Δ ABC
AC2= AB2 + BC2
Putting the value of base (AB) and perpendicular (BC) to get the hypotenuse (AC);
AC2 = 122 + 52
AC2= 144 + 25
AC2 = 169
AC = √169
AC = 13
Hence, Hypotenuse = 13
By definition,
Since, sin θ = perpendicular/Hypotenuse
∴ sin θ= 5/13
Since, cosec θ = 1/sin θ
Also, cosec θ= Hypotenuse/Perpendicualar
∴ cosec θ = 13/5
Since, cos θ = Base/Hypotenuse
∴ cos θ = 12/13
Since, sec θ = 1/cosθ
Also, sec θ = Hypotenuse/Base
∴ sec θ = 13/12
Since, tanθ = 1/cot θ
Also, tan θ = Perpendicular/Base
∴ tan θ = 5/12
(x) sec θ = 13/5
Solution:
We have, sec θ = 13/5…….… (1)
By definition,
sec θ = Hypotenuse/Base…………. (2)
On Comparing eq. (1) and (2), we get
Base = 5 and Hypotenuse = 13
Now, using Pythagoras theorem in Δ ABC
AC2 = AB2 + BC2
And. putting the value of base side (AB) and hypotenuse (AC) to get the perpendicular side (BC)
132 = 52 + BC2
BC2 = 132 – 52
BC2=169 – 25
BC2= 144
BC= √144
BC = 12
Hence, Perpendicular = 12
By definition,
Since, sin θ = perpendicular/Hypotenuse
∴ sin θ= 12/13
Since, cosec θ= 1/ sin θ
Also, cosec θ= Hypotenuse/Perpendicualar
∴ cosec θ = 13/12
Since, cos θ= 1/sec θ
Also, cos θ = Base/Hypotenuse
∴ cos θ = 5/13
Since, tan θ = Perpendicular/Base
∴ tan θ = 12/5
Since, cot θ = 1/tan θ
Also, cot θ = Base/Perpendicular
∴ cot θ = 5/12
(xi) cosec θ = √10
Solution:
We have, cosec θ = √10/1 ……..… (1)
By definition,
cosec θ = Hypotenuse/ Perpendicualar …….….(2)
And, cosecθ = 1/sin θ
On comparing eq.(1) and(2), we get
Perpendicular side = 1 and Hypotenuse = √10
Now, using Pythagoras theorem in Δ ABC
AC2 = AB2 + BC2
Putting the value of perpendicular (BC) and hypotenuse (AC) to get the base side (AB)
(√10)2 = AB2 + 12
AB2= (√10)2 – 12
AB2= 10 – 1
AB = √9
AB = 3
So, Base side = 3
By definition,
Since, sin θ = Perpendicular/Hypotenuse
∴ sin θ = 1/√10
Since, cos θ = Base/Hypotenuse
∴ cos θ = 3/√10
Since, sec θ = 1/cos θ
Also, sec θ = Hypotenuse/Base
∴ sec θ = √10/3
Since, tan θ = Perpendicular/Base
∴ tan θ = 1/3
Since, cot θ = 1/tan θ
∴ cot θ = 3/1
(xii) cos θ =12/15
Solution:
We have; cos θ = 12/15 ………. (1)
By definition,
cos θ = Base/Hypotenuse……… (2)
By comparing eq. (1) and (2), we get;
Base =12 and Hypotenuse = 15
Now, using Pythagoras theorem in Δ ABC, we get
AC2 = AB2+ BC2
Putting the value of base (AB) and hypotenuse (AC) to get the perpendicular (BC);
152 = 122 + BC2
BC2 = 152 – 122
BC2 = 225 – 144
BC 2= 81
BC = √81
BC = 9
So, Perpendicular = 9
By definition,
Since, sin θ = perpendicular/Hypotenuse
∴ sin θ = 9/15 = 3/5
Since, cosec θ = 1/sin θ
Also, cosec θ = Hypotenuse/Perpendicualar
∴ cosec θ= 15/9 = 5/3
Since, sec θ = 1/cos θ
Also, sec θ = Hypotenuse/Base
∴ sec θ = 15/12 = 5/4
Since, tan θ = Perpendicular/Base
∴ tan θ = 9/12 = 3/4
Since, cot θ = 1/tan θ
Also, cot θ = Base/Perpendicular
∴ cot θ = 12/9 = 4/3
2. In a △ ABC, right angled at B, AB = 24 cm , BC = 7 cm. Determine
(i) sin A , cos A (ii) sin C, cos C
Solution:

(i) Given: In △ABC, AB = 24 cm, BC = 7cm and ∠ABC = 90o
To find: sin A, cos A
By using Pythagoras theorem in △ABC we have
AC2 = AB2 + BC2
AC2 = 242 + 72
AC2 = 576 + 49
AC2= 625
AC = √625
AC= 25
Hence, Hypotenuse = 25
By definition,
sin A = Perpendicular side opposite to angle A/ Hypotenuse
sin A = BC/ AC
sin A = 7/ 25
And,
cos A = Base side adjacent to angle A/Hypotenuse
cos A = AB/ AC
cos A = 24/ 25
(ii) Given: In △ABC , AB = 24 cm and BC = 7cm and ∠ABC = 90o
To find: sin C, cos C
By using Pythagoras theorem in △ABC we have
AC2 = AB2 + BC2
AC2 = 242 + 72
AC2 = 576 + 49
AC2= 625
AC = √625
AC= 25
Hence, Hypotenuse = 25
By definition,
sin C = Perpendicular side opposite to angle C/Hypotenuse
sin C = AB/ AC
sin C = 24/ 25
And,
cos C = Base side adjacent to angle C/Hypotenuse
cos A = BC/AC
cos A = 7/25
3. In fig. 5.37, find tan P and cot R. Is tan P = cot R?
Solution:

By using Pythagoras theorem in △PQR, we have
PR2 = PQ2 + QR2
Putting the length of given side PR and PQ in the above equation
132 = 122 + QR2
QR2 = 132 – 122
QR2 = 169 – 144
QR2 = 25
QR = √25 = 5
By definition,
tan P = Perpendicular side opposite to P/ Base side adjacent to angle P
tan P = QR/PQ
tan P = 5/12 ………. (1)
And,
cot R= Base/Perpendicular
cot R= QR/PQ
cot R= 5/12 …. (2)
When comparing equation (1) and (2), we can see that R.H.S of both the equation is equal.
Therefore, L.H.S of both equations should also be equal.
∴ tan P = cot R
Yes, tan P = cot R = 5/12
4. If sin A = 9/41, compute cos A and tan A.
Solution:

Given that, sin A = 9/41 …………. (1)
Required to find: cos A, tan A
By definition, we know that
sin A = Perpendicular/ Hypotenuse……………(2)
On Comparing eq. (1) and (2), we get;
Perpendicular side = 9 and Hypotenuse = 41
Let’s construct △ABC as shown below,
And, here the length of base AB is unknown.
Thus, by using Pythagoras theorem in △ABC, we get;
AC2 = AB2 + BC2
412 = AB2 + 92
AB2 = 412 – 92
AB2 = 168 – 81
AB= 1600
AB = √1600
AB = 40
⇒ Base of triangle ABC, AB = 40
We know that,
cos A = Base/ Hypotenuse
cos A =AB/AC
cos A =40/41
And,
tan A = Perpendicular/ Base
tan A = BC/AB
tan A = 9/40
5. Given 15cot A= 8, find sin A and sec A.
Solution

We have, 15cot A = 8
Required to find: sin A and sec A
As, 15 cot A = 8
⇒ cot A = 8/15 …….(1)
And we know,
cot A = 1/tan A
Also by definition,
Cot A = Base side adjacent to ∠A/ Perpendicular side opposite to ∠A …. (2)
On comparing equation (1) and (2), we get;
Base side adjacent to ∠A = 8
Perpendicular side opposite to ∠A = 15
So, by using Pythagoras theorem to △ABC, we have
AC2 = AB2 +BC2
Substituting values for sides from the figure
AC2 = 82 + 152
AC2 = 64 + 225
AC2 = 289
AC = √289
AC = 17
Therefore, hypotenuse =17
By definition,
sin A = Perpendicular/Hypotenuse
⇒ sin A= BC/AC
sin A= 15/17 (using values from the above)
Also,
sec A= 1/ cos A
⇒ secA = Hypotenuse/ Base side adjacent to ∠A
∴ sec A= 17/8
6. In △PQR, right-angled at Q, PQ = 4cm and RQ = 3 cm. Find the value of sin P, sin R, sec P and sec R.
Solution:

Given:
△PQR is right-angled at Q.
PQ = 4cm
RQ = 3cm
Required to find: sin P, sin R, sec P, sec R
Given △PQR,
By using Pythagoras theorem to △PQR, we get
PR2 = PQ2 +RQ2
Substituting the respective values,
PR2 = 42 +32
PR2 = 16 + 9
PR2 = 25
PR = √25
PR = 5
⇒ Hypotenuse =5
By definition,
sin P = Perpendicular side opposite to angle P/ Hypotenuse
sin P = RQ/ PR
⇒ sin P = 3/5
And,
sin R = Perpendicular side opposite to angle R/ Hypotenuse
sin R = PQ/ PR
⇒ sin R = 4/5
And,
sec P=1/cos P
secP = Hypotenuse/ Base side adjacent to ∠P
sec P = PR/ PQ
⇒ sec P = 5/4
Now,
sec R = 1/cos R
secR = Hypotenuse/ Base side adjacent to ∠R
sec R = PR/ RQ
⇒ sec R = 5/3
7. If cot θ = 7/8, evaluate
(i) (1+sin θ)(1–sin θ)/ (1+cos θ)(1–cos θ)
(ii) cot2 θ
Solution:
(i) Required to evaluate: , given = cot θ = 7/8
, given = cot θ = 7/8
Taking the numerator, we have
(1+sin θ)(1–sin θ) = 1 – sin2 θ [Since, (a+b)(a-b) = a2 – b2]
Similarly,
(1+cos θ)(1–cos θ) = 1 – cos2 θ
We know that,
sin2 θ + cos2 θ = 1
⇒ 1 – cos2 θ = sin2 θ
And,
1 – sin2 θ = cos2 θ
Thus,
(1+sin θ)(1 –sin θ) = 1 – sin2 θ = cos2 θ
(1+cos θ)(1–cos θ) = 1 – cos2 θ = sin2 θ
⇒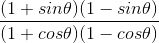
= cos2 θ/ sin2 θ
= (cos θ/sin θ)2
And, we know that (cos θ/sin θ) = cot θ
⇒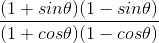
= (cot θ)2
= (7/8)2
= 49/ 64
(ii) Given,
cot θ = 7/8
So, by squaring on both sides we get
(cot θ)2 = (7/8)2
∴ cot θ2 = 49/64
8. If 3cot A = 4, check whether (1–tan2A)/(1+tan2A) = (cos2A – sin2A) or not.
Solution:

Given,
3cot A = 4
⇒ cot A = 4/3
By definition,
tan A = 1/ Cot A = 1/ (4/3)
⇒ tan A = 3/4
Thus,
Base side adjacent to ∠A = 4
Perpendicular side opposite to ∠A = 3
In ΔABC, Hypotenuse is unknown
Thus, by applying Pythagoras theorem in ΔABC
We get
AC2 = AB2 + BC2
AC2 = 42 + 32
AC2 = 16 + 9
AC2 = 25
AC = √25
AC = 5
Hence, hypotenuse = 5
Now, we can find that
sin A = opposite side to ∠A/ Hypotenuse = 3/5
And,
cos A = adjacent side to ∠A/ Hypotenuse = 4/5
Taking the LHS,

Thus, LHS = 7/25
Now, taking RHS
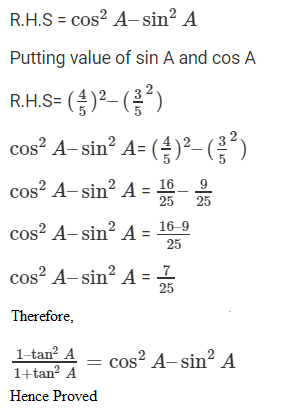
9. If tan θ = a/b, find the value of (cos θ + sin θ)/ (cos θ – sin θ)
Solution:
Given,
tan θ = a/b
And, we know by definition that
tan θ = opposite side/ adjacent side
Thus, by comparison
Opposite side = a and adjacent side = b
To find the hypotenuse, we know that by Pythagoras theorem that
Hypotenuse2 = opposite side2 + adjacent side2
⇒ Hypotenuse = √(a2 + b2)
So, by definition
sin θ = opposite side/ Hypotenuse
sin θ = a/ √(a2 + b2)
And,
cos θ = adjacent side/ Hypotenuse
cos θ = b/ √(a2 + b2)
Now,
After substituting for cos θ and sin θ, we have


∴
Hence Proved.
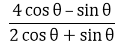
10. If 3 tan θ = 4, find the value of
Solution:
Given, 3 tan θ = 4
⇒ tan θ = 4/3

From, let’s divide the numerator and denominator by cos θ.
We get,
(4 – tan θ) / (2 + tan θ)
⇒ (4 – (4/3)) / (2 + (4/3)) [using the value of tan θ]
⇒ (12 – 4) / (6 + 4) [After taking LCM and cancelling it]
⇒ 8/10 = 4/5

∴ = 4/5

11. If 3 cot θ = 2, find the value of
Solution:
Given, 3 cot θ = 2
⇒ cot θ = 2/3

From, let’s divide the numerator and denominator by sin θ.
We get,
(4 –3 cot θ) / (2 + 6 cot θ)
⇒ (4 – 3(2/3)) / (2 + 6(2/3)) [using the value of tan θ]
⇒ (4 – 2) / (2 + 4) [After taking LCM and simplifying it]
⇒ 2/6 = 1/3

∴ = 1/3

12. If tan θ = a/b, prove that
Solution:
Given, tan θ = a/b

From LHS, let’s divide the numerator and denominator by cos θ.
And we get,
(a tan θ – b) / (a tan θ + b)
⇒ (a(a/b) – b) / (a(a/b) + b) [using the value of tan θ]
⇒ (a2 – b2)/b2 / (a2 + b2)/b2 [After taking LCM and simplifying it]
⇒ (a2 – b2)/ (a2 + b2)
= RHS
– Hence Proved

13. If sec θ = 13/5, show that
Solution:

Given,
sec θ = 13/5
We know that,
sec θ = 1/ cos θ
⇒ cos θ = 1/ sec θ = 1/ (13/5)
∴ cos θ = 5/13 ……. (1)
By definition,
cos θ = adjacent side/ hypotenuse ….. (2)
Comparing (1) and (2), we have
Adjacent side = 5 and hypotenuse = 13
By Pythagoras theorem,
Opposite side = √((hypotenuse) 2 – (adjacent side)2)
= √(132 – 52)
= √(169 – 25)
= √(144)
= 12
Thus, opposite side = 12
By definition,
tan θ = opposite side/ adjacent side
∴ tan θ = 12/ 5

From, let’s divide the numerator and denominator by cos θ.
We get,
(2 tan θ – 3) / (4 tan θ – 9)
⇒ (2(12/5) – 3) / (4(12/5) – 9) [using the value of tan θ]
⇒ (24 – 15) / (48 – 45) [After taking LCM and cancelling it]
⇒ 9/3 = 3

∴ = 3
14. If cos θ = 12/13, show that sin θ(1 – tan θ) = 35/156
Solution:

Given, cos θ = 12/13…… (1)
By definition we know that,
cos θ = Base side adjacent to ∠θ / Hypotenuse……. (2)
When comparing equation (1) and (2), we get
Base side adjacent to ∠θ = 12 and Hypotenuse = 13
From the figure,
Base side BC = 12
Hypotenuse AC = 13
Side AB is unknown here and it can be found by using Pythagoras theorem
Thus by applying Pythagoras theorem,
AC2 = AB2 + BC2
132 = AB2 + 122
Therefore,
AB2 = 132 – 122
AB2 = 169 – 144
AB2 = 25
AB = √25
AB = 5 …. (3)
Now, we know that
sin θ = Perpendicular side opposite to ∠θ / Hypotenuse
Thus, sin θ = AB/AC [from figure]
⇒ sin θ = 5/13… (4)
And, tan θ = sin θ / cos θ = (5/13) / (12/13)
⇒ tan θ = 12/13… (5)
Taking L.H.S we have
L.H.S = sin θ (1 – tan θ)
Substituting the value of sin θ and tan θ from equation (4) and (5)
We get,

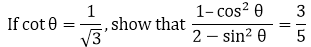
15.
Solution:

Given, cot θ = 1/3……. (1)
By definition we know that,
cot θ = 1/ tan θ
And, since tan θ = perpendicular side opposite to ∠θ / Base side adjacent to ∠θ
⇒ cot θ = Base side adjacent to ∠θ / perpendicular side opposite to ∠θ …… (2)
[Since they are reciprocal to each other]
On comparing equation (1) and (2), we get
Base side adjacent to ∠θ = 1 and Perpendicular side opposite to ∠θ = √3
Therefore, the triangle formed is,
On substituting the values of known sides as AB = √3 and BC = 1
AC2 = (√3) + 1
AC2 = 3 + 1
AC2 = 4
AC = √4
Therefore, AC = 2 … (3)
Now, by definition
sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC
⇒ sin θ = √3/ 2 ……(4)
And, cos θ = Base side adjacent to ∠θ / Hypotenuse = BC / AC
⇒ cos θ = 1/ 2 ….. (5)
Now, taking L.H.S we have

Substituting the values from equation (4) and (5), we have


16.
Solution:
Given, tan θ = 1/ √7 …..(1)

By definition, we know that
tan θ = Perpendicular side opposite to ∠θ / Base side adjacent to ∠θ ……(2)
On comparing equation (1) and (2), we have
Perpendicular side opposite to ∠θ = 1
Base side adjacent to ∠θ = √7
Thus, the triangle representing ∠ θ is,
Hypotenuse AC is unknown and it can be found by using Pythagoras theorem
By applying Pythagoras theorem, we have
AC2 = AB2 + BC2
AC2 = 12 + (√7)2
AC 2 = 1 + 7
AC2 = 8
AC = √8
⇒ AC = 2√2
By definition,
sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC
⇒ sin θ = 1/ 2√2
And, since cosec θ = 1/sin θ
⇒ cosec θ = 2√2 …….. (3)
Now,
cos θ = Base side adjacent to ∠θ / Hypotenuse = BC / AC
⇒ cos θ = √7/ 2√2
And, since sec θ = 1/ sin θ
⇒ sec θ = 2√2/ √7 ……. (4)
Taking the L.H.S of the equation,

Substituting the value of cosec θ and sec θ from equation (3) and (4), we get


17. If sec θ = 5/4, find the value of
Solution:
Given,
sec θ = 5/4
We know that,
sec θ = 1/ cos θ
⇒ cos θ = 1/ (5/4) = 4/5 …… (1)
By definition,
cos θ = Base side adjacent to ∠θ / Hypotenuse …. (2)
On comparing equation (1) and (2), we have
Hypotenuse = 5
Base side adjacent to ∠θ = 4
Thus, the triangle representing ∠ θ is ABC.
Perpendicular side opposite to ∠θ, AB is unknown and it can be found by using Pythagoras theorem
By applying Pythagoras theorem, we have
AC2 = AB2 + BC2
AB2 = AC2 + BC2
AB2 = 52 – 42
AB2 = 25 – 16
AB = √9
⇒ AB = 3
By definition,
sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC
⇒ sin θ = 3/ 5 …..(3)
Now, tan θ = Perpendicular side opposite to ∠θ / Base side adjacent to ∠θ
⇒ tan θ = 3/ 4 ……(4)
And, since cot θ = 1/ tan θ
⇒ cot θ = 4/ 3 ……(5)
Now,
Substituting the value of sin θ, cos θ, cot θ and tan θ from the equations (1), (3), (4) and (5) we have,

= 12/7
Therefore,


18. If tan θ = 12/13, find the value of
Solution:
Given,
tan θ = 12/13 …….. (1)
We know that by definition,
tan θ = Perpendicular side opposite to ∠θ / Base side adjacent to ∠θ …… (2)
On comparing equation (1) and (2), we have
Perpendicular side opposite to ∠θ = 12
Base side adjacent to ∠θ = 13
Thus, in the triangle representing ∠ θ we have,
Hypotenuse AC is the unknown and it can be found by using Pythagoras theorem
So by applying Pythagoras theorem, we have
AC2 = 122 + 132
AC 2 = 144 + 169
AC2 = 313
⇒ AC = √313
By definition,
sin θ = Perpendicular side opposite to ∠θ / Hypotenuse = AB / AC
⇒ sin θ = 12/ √313…..(3)
And, cos θ = Base side adjacent to ∠θ / Hypotenuse = BC / AC
⇒ cos θ = 13/ √313 …..(4)
Now, substituting the value of sin θ and cos θ from equation (3) and (4) respectively in the equation below

Therefore,

RD Sharma Solutions for Class 10 Maths Chapter 5 Exercise 5.2 Page No: 5.41
Evaluate each of the following:
1. sin 45∘ sin 30∘ + cos 45∘ cos 30∘
Solution:
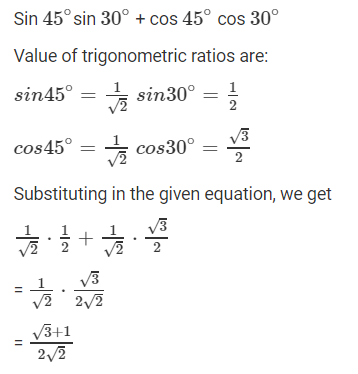
2. sin 60∘ cos 30∘ + cos 60∘ sin 30∘
Solution:

3. cos 60∘ cos 45∘ – sin 60∘ sin 45∘
Solution:

4. sin2 30∘ + sin2 45∘ + sin2 60∘ + sin2 90∘
Solution:

5. cos2 30∘ + cos2 45∘ + cos2 60∘ + cos2 90∘
Solution:

6. tan2 30∘ + tan2 45∘ + tan2 60∘
Solution:

7. 2sin2 30∘ − 3cos2 45∘ + tan2 60∘
Solution:

8. sin2 30∘ cos245∘ + 4tan2 30∘ + (1/2) sin2 90∘ − 2cos2 90∘ + (1/24) cos20∘
Solution:


9. 4(sin4 60∘ + cos4 30∘) − 3(tan2 60∘ − tan2 45∘) + 5cos2 45∘
Solution:

10. (cosec2 45∘ sec2 30∘)(sin2 30∘ + 4cot2 45∘ − sec2 60∘)
Solution:

11. cosec3 30∘ cos60∘ tan3 45∘ sin2 90∘ sec2 45∘ cot30∘
Solution:

12. cot2 30∘ − 2cos2 60∘ − (3/4)sec2 45∘ – 4sec2 30∘
Solution:
Using trigonometric values, we have

13. (cos0∘ + sin45∘ + sin30∘)(sin90∘ − cos45∘ + cos60∘)
Solution:
(cos0∘ + sin45∘ + sin30∘)(sin90∘ − cos45∘ + cos60∘)
Using trigonometric values, we have


15. 4/cot2 30∘ + 1/sin2 60∘ − cos2 45∘
Solution:

16. 4(sin4 30∘ + cos2 60∘) − 3(cos2 45∘ − sin2 90∘) − sin2 60∘
Solution:
Using trigonometric values, we have


17.
Solution:
Using trigonometric values, we have

 18.
18.
Solution:
Using trigonometric values, we have


19.
Solution:
Using trigonometric values, we have

Find the value of x in each of the following: (20-25)
20. 2sin 3x = √3
Solution:
Given,
2 sin 3x = √3
sin 3x = √3/2
sin 3x = sin 60°
3x = 60°
x = 20°
RD Sharma Solutions for Class 10 Maths Chapter 5 Exercise 5.3 Page No: 5.52
1. Evalute the following:
(i) sin 20o/ cos 70o
(ii) cos 19o/ sin 71o
(iii) sin 21o/ cos 69o
(iv) tan 10o/ cot 80o
(v) sec 11o/ cosec 79o
Solution:
(i) We have,
sin 20o/ cos 70o = sin (90o – 70o)/ cos 70o = cos 70o/ cos70o = 1 [∵ sin (90 – θ) = cos θ]
(ii) We have,
cos 19o/ sin 71o = cos (90o – 71o)/ sin 71o = sin 71o/ sin 71o = 1 [∵ cos (90 – θ) = sin θ]
(iii) We have,
sin 21o/ cos 69o = sin (90o – 69o)/ cos 69o = cos 69o/ cos69o = 1 [∵ sin (90 – θ) = cos θ]
(iv) We have,
tan 10o/ cot 80o = tan (90o – 10o) / cot 80o = cot 80o/ cos80o = 1 [∵ tan (90 – θ) = cot θ]
(v) We have,
sec 11o/ cosec 79o = sec (90o – 79o)/ cosec 79o = cosec 79o/ cosec 79o = 1
[∵ sec (90 – θ) = cosec θ]
2. Evaluate the following:

Solution:
We have, [∵ sin (90 – θ) = cos θ and cos (90 – θ) = sin θ]

= 12 + 12 = 1 + 1
= 2
(ii) cos 48°- sin 42°
Solution:
We know that, cos (90° − θ) = sin θ.
So,
cos 48° – sin 42° = cos (90° − 42°) – sin 42° = sin 42° – sin 42°= 0
Thus the value of cos 48° – sin 42° is 0.

Solution:
We have, [∵ cot (90 – θ) = tan θ and cos (90 – θ) = sin θ]

= 1 – 1/2(1)
= 1/2

Solution:
We have, [∵ sin (90 – θ) = cos θ and cos (90 – θ) = sin θ]

= 1 – 1
= 0

Solution:
We have, [∵ cot (90 – θ) = tan θ and tan (90 – θ) = cot θ]

= tan (90o – 35o)/ cot 55o + cot (90o – 12o)/ tan 12o – 1
= cot 55o/ cot 55o + tan 12o/ tan 12o – 1
= 1 + 1 – 1
= 1

Solution:
We have , [∵ sin (90 – θ) = cos θ and sec (90 – θ) = cosec θ]

= sec (90o – 20o)/ cosec 20o + sin (90o – 31o)/ cos 31o
= cosec 20o/ cosec 20o + cos 12o/ cos 12o
= 1 + 1
= 2
(vii) cosec 31° – sec 59°
Solution:
We have,
cosec 31° – sec 59°
Since, cosec (90 – θ) = cos θ
So,
cosec 31° – sec 59° = cosec (90° – 59o) – sec 59° = sec 59° – sec 59° = 0
Thus,
cosec 31° – sec 59° = 0
(viii) (sin 72° + cos 18°) (sin 72° – cos 18°)
Solution:
We know that,
sin (90 – θ) = cos θ
So, the given can be expressed as
(sin 72° + cos 18°) (sin (90 – 18)° – cos 18°)
= (sin 72° + cos 18°) (cos 18° – cos 18°)
= (sin 72° + cos 18°) x 0
= 0
(ix) sin 35° sin 55° – cos 35° cos 55°
Solution:
We know that,
sin (90 – θ) = cos θ
So, the given can be expressed as
sin (90 – 55)° sin (90 – 35)° – cos 35° cos 55°
= cos 55° cos 35° – cos 35° cos 55°
= 0
(x) tan 48° tan 23° tan 42° tan 67°
Solution:
We know that,
tan (90 – θ) = cot θ
So, the given can be expressed as
tan (90 – 42)° tan (90 – 67)° tan 42° tan 67°
= cot 42° cot 67° tan 42° tan 67°
= (cot 42° tan 42°)(cot 67° tan 67°)
= 1 x 1 [∵ tan θ x cot θ = 1]
= 1
(xi) sec 50° sin 40° + cos 40° cosec 50°
Solution:
We know that,
sin (90 – θ) = cos θ and cos (90 – θ) = sin θ
So, the given can be expressed as
sec 50° sin (90 – 50)° + cos (90 – 50)° cosec 50°
= sec 50° cos 50° + sin 50° cosec 50°
= 1 + 1 [∵ sin θ x cosec θ = 1 and cos θ x sec θ = 1]
= 2
3. Express each one of the following in terms of trigonometric ratios of angles lying between 0o and 45o
(i) sin 59o + cos 56o (ii) tan 65o + cot 49o (iii) sec 76o + cosec 52o
(iv) cos 78o + sec 78o (v) cosec 54o + sin 72o (vi) cot 85o + cos 75o
(vii) sin 67o + cos 75o
Solution:
Using the below trigonometric ratios of complementary angles, we find the required
sin (90 – θ) = cos θ cosec (90 – θ) = sec θ
cos (90 – θ) = sin θ sec (90 – θ) = cosec θ
tan (90 – θ) = cot θ cot (90 – θ) = tan θ
(i) sin 59o + cos 56o = sin (90 – 31)o + cos (90 – 34)o = cos 31o + sin 34o
(ii) tan 65o + cot 49o = tan (90 – 25)o + cot (90 -31)o = cot 25o + tan 31o
(iii) sec 76o + cosec 52o = sec (90 – 14)o + cosec (90 – 38)o = cosec 14o + sec 38o
(iv) cos 78o + sec 78o = cos (90 – 12)o + sec (90 – 12)o = sin 12o + cosec 12o
(v) cosec 54o + sin 72o = cosec (90 – 36)o + sin (90 – 18)o = sec 36o + cos 18o
(vi) cot 85o + cos 75o = cot (90 – 5)o + cos (90 – 15)o = tan 5o + sin 15o
4. Express cos 75o + cot 75o in terms of angles between 0o and 30o.
Solution:
Given,
cos 75o + cot 75o
Since, cos (90 – θ) = sin θ and cot (90 – θ) = tan θ
cos 75o + cot 75o = cos (90 – 15)o + cot (90 – 15)o = sin 15o + tan 15o
Hence, cos 75o + cot 75o can be expressed as sin 15o + tan 15o
5. If sin 3A = cos (A – 26o), where 3A is an acute angle, find the value of A.
Solution:
Given,
sin 3A = cos (A – 26o)
Using cos (90 – θ) = sin θ, we have
sin 3A = sin (90o – (A – 26o))
Now, comparing both L.H.S and R.H.S
3A = 90o – (A – 26o)
3A + (A – 26o) = 90o
4A – 26o = 90o
4A = 116o
A = 116o/4
∴ A = 29o
6. If A, B, C are the interior angles of a triangle ABC, prove that
(i) tan ((C + A)/ 2) = cot (B/2) (ii) sin ((B + C)/ 2) = cos (A/2)
Solution:
We know that, in triangle ABC the sum of the angles i.e A + B + C = 180o
So, C + A = 180o – B ⇒ (C + A)/2 = 90o – B/2 …… (i)
And, B + C = 180o – A ⇒ (B + C)/2 = 90o – A/2 ……. (ii)
(i) L.H.S = tan ((C + A)/ 2)
⇒ tan ((C + A)/ 2) = tan (90o – B/2) [From (i)]
= cot (B/2) [∵ tan (90 – θ) = cot θ]
= R.H.S
- Hence Proved
(ii) L.H.S = sin ((B + C)/2)
⇒ tan ((B + C)/ 2) = tan (90o – A/2) [From (ii)]
= cot (B/2) [∵ tan (90 – θ) = cot θ]
= R.H.S
- Hence Proved
7. Prove that:
(i) tan 20° tan 35° tan 45° tan 55° tan 70° = 1
(ii) sin 48° sec 48° + cos 48° cosec 42° = 2

Solution:
(i) Taking L.H.S = tan 20° tan 35° tan 45° tan 55° tan 70°
= tan (90° − 70°) tan (90° − 55°) tan 45°tan 55° tan70°
= cot 70°cot 55° tan 45° tan 55° tan 70° [∵ tan (90 – θ) = cot θ]
= (tan 70°cot 70°)(tan 55°cot 55°) tan 45° [∵ tan θ x cot θ = 1]
= 1 × 1 × 1 = 1
- Hence proved
(ii) Taking L.H.S = sin 48° sec 48° + cos 48° cosec 42°
= sin 48° sec (90° − 48°) cos 48° cosec (90° − 48°)
[∵sec (90 – θ) = cosec θ and cosec (90 – θ) = sec θ]
= sin 48°cosec 48° + cos 48°sec 48° [∵ cosec θ x sin θ = 1 and cos θ x sec θ = 1]
= 1 + 1 = 2
- Hence proved
(iii) Taking the L.H.S,

= 1 + 1 – 2
= 2 – 2
= 0
- Hence proved
(iv) Taking L.H.S,

= 1 + 1
= 2
- Hence proved
8. Prove the following:
(i) sinθ sin (90o – θ) – cos θ cos (90o – θ) = 0
Solution:
Taking the L.H.S,
sinθ sin (90o – θ) – cos θ cos (90o – θ)
= sin θ cos θ – cos θ sin θ [∵ sin (90 – θ) = cos θ and cos (90 – θ) = sin θ]
= 0
 (ii)
(ii)
Solution:
Taking the L.H.S,

 [∵ cosec θ x sin θ = 1 and cos θ x sec θ = 1]
[∵ cosec θ x sin θ = 1 and cos θ x sec θ = 1]
= 1 + 1
= 2 = R.H.S
- Hence Proved
 (iii)
(iii)
Solution:
Taking the L.H.S, [∵ tan (90o – θ) = cot θ]

= 0 = R.H.S
- Hence Proved
 (iv)
(iv)
Solution:
Taking L.H.S, [∵ sin (90 – θ) = cos θ and cos (90 – θ) = sin θ]

= sin2 A = R.H.S
- Hence Proved
(v) sin (50o + θ) – cos (40o – θ) + tan 1o tan 10o tan 70o tan 80o tan 89o = 1
Solution:
Taking the L.H.S,
= sin (50o + θ) – cos (40o – θ) + tan 1o tan 10o tan 20o tan 70o tan 80o tan 89o
= sin (50o + θ) – sin (90o – (40o – θ)) + tan (90 – 89)o tan (90 – 80)o tan (90 – 70)o tan 70o tan 80o tan 89o [∵ sin (90 – θ) = cos θ]
= sin (50o + θ) – sin (50o + θ) + cot 89o cot 80o cot 70o tan 70o tan 80o tan 89o
[∵ tan (90o – θ) = cot θ]
= 0 + (cot 89o x tan 89o) (cot 80o x tan 80o) (cot 70o x tan 70o)
= 0 + 1 x 1 x 1 [∵ tan θ x cot θ = 1]
= 1= R.H.S
- Hence Proved
