RD Sharma Solutions for Class 8 Chapter 8 Division of Algebraic Expressions Free Online
EXERCISE 8.1 PAGE NO: 8.2
1. Write the degree of each of the following polynomials:
(i) 2x3 + 5x2 – 7
(ii) 5x2 – 3x + 2
(iii) 2x + x2 – 8
(iv) 1/2y7 – 12y6 + 48y5 – 10
(v) 3x3 + 1
(vi) 5
(vii) 20x3 + 12x2y2 – 10y2 + 20
Solution:
(i) 2x3 + 5x2 – 7
We know that in a polynomial, degree is the highest power of the variable.
The degree of the polynomial, 2x3 + 5x2 – 7 is 3.
(ii) 5x2 – 3x + 2
The degree of the polynomial, 5x2 – 3x + 2 is 2.
(iii) 2x + x2 – 8
The degree of the polynomial, 2x + x2 – 8 is 2.
(iv) 1/2y7 – 12y6 + 48y5 – 10
The degree of the polynomial, 1/2y7 – 12y6 + 48y5 – 10 is 7.
(v) 3x3 + 1
The degree of the polynomial, 3x3 + 1 is 3
(vi) 5
The degree of the polynomial, 5 is 0 (since 5 is a constant number).
(vii) 20x3 + 12x2y2 – 10y2 + 20
The degree of the polynomial, 20x3 + 12x2y2 – 10y2 + 20 is 4.
2. Which of the following expressions are not polynomials?
(i) x2 + 2x-2
(ii) √(ax) + x2 – x3
(iii) 3y3 – √5y + 9
(iv) ax1/2 + ax + 9x2 + 4
(v) 3x-3 + 2x-1 + 4x + 5
Solution:
(i) x2 + 2x-2
The given expression is not a polynomial.
Because a polynomial does not contain any negative powers or fractions.
(ii) √(ax) + x2 – x3
The given expression is a polynomial.
Because the polynomial has positive powers.
(iii) 3y3 – √5y + 9
The given expression is a polynomial.
Because the polynomial has positive powers.
(iv) ax1/2 + ax + 9x2 + 4
The given expression is not a polynomial.
Because a polynomial does not contain any negative powers or fractions.
(v) 3x-3 + 2x-1 + 4x + 5
The given expression is not a polynomial.
Because a polynomial does not contain any negative powers or fractions.
3. Write each of the following polynomials in the standard from. Also, write their degree:
(i) x2 + 3 + 6x + 5x4
(ii) a2 + 4 + 5a6
(iii) (x3 – 1) (x3 – 4)
(iv) (y3 – 2) (y3 + 11)
(v) (a3 – 3/8) (a3 + 16/17)
(vi) (a + 3/4) (a + 4/3)
Solution:
(i) x2 + 3 + 6x + 5x4
The standard form of the polynomial is written in either increasing or decreasing order of their powers.
3 + 6x + x2 + 5x4 or 5x4 + x2 + 6x + 3
The degree of the given polynomial is 4.
(ii) a2 + 4 + 5a6
The standard form of the polynomial is written in either increasing or decreasing order of their powers.
4 + a2 + 5a6 or 5a6 + a2 + 4
The degree of the given polynomial is 6.
(iii) (x3 – 1) (x3 – 4)
x6 – 4x3 – x3 + 4
x6 – 5x3 + 4
The standard form of the polynomial is written in either increasing or decreasing order of their powers.
x6 – 5x3 + 4 or 4 – 5x3 + x6
The degree of the given polynomial is 6.
(iv) (y3 – 2) (y3 + 11)
y6 + 11y3 – 2y3 – 22
y6 + 9y3 – 22
The standard form of the polynomial is written in either increasing or decreasing order of their powers.
y6 + 9y3 – 22 or -22 + 9y3 + y6
The degree of the given polynomial is 6.
(v) (a3 – 3/8) (a3 + 16/17)
a6 + 16a3/17 – 3a3/8 – 6/17
a6 + 27/136a3 – 48/136
The standard form of the polynomial is written in either increasing or decreasing order of their powers.
a6 + 27/136a3 – 48/136 or -48/136 + 27/136a3 + a6
The degree of the given polynomial is 6.
(vi) (a + 3/4) (a + 4/3)
a2 + 4a/3 + 3a/4 + 1
a2 + 25a/12 + 1
The standard form of the polynomial is written in either increasing or decreasing order of their powers.
a2 + 25a/12 + 1 or 1 + 25a/12 + a2
The degree of the given polynomial is 2.
EXERCISE 8.2 PAGE NO: 8.4
Divide:
1. 6x3y2z2 by 3x2yz
Solution:
We have,
6x3y2z2 / 3x2yz
By using the formula an / am = an-m
6/3 x3-2 y2-1 z2-1
2xyz
2. 15m2n3 by 5m2n2
Solution:
We have,
15m2n3 / 5m2n2
By using the formula an / am = an-m
15/5 m2-2 n3-2
3n
3. 24a3b3 by -8ab
Solution:
We have,
24a3b3 / -8ab
By using the formula an / am = an-m
24/-8 a3-1 b3-1
-3a2b2
4. -21abc2 by 7abc
Solution:
We have,
-21abc2 / 7abc
By using the formula an / am = an-m
-21/7 a1-1 b1-1 c2-1
-3c
5. 72xyz2 by -9xz
Solution:
We have,
72xyz2 / -9xz
By using the formula an / am = an-m
72/-9 x1-1 y z2-1
-8yz
6. -72a4b5c8 by -9a2b2c3
Solution:
We have,
-72a4b5c8 / -9a2b2c3
By using the formula an / am = an-m
-72/-9 a4-2 b5-2 c8-3
8a2b3c5
Simplify:
7. 16m3y2 / 4m2y
Solution:
We have,
16m3y2 / 4m2y
By using the formula an / am = an-m
16/4 m3-2 y2-1
4my
8. 32m2n3p2 / 4mnp
Solution:
We have,
32m2n3p2 / 4mnp
By using the formula an / am = an-m
32/4 m2-1 n3-1 p2-1
8m2n2p
EXERCISE 8.3 PAGE NO: 8.6
Divide:
1. x + 2x2 + 3x4 – x5 by 2x
Solution:
We have,
(x + 2x2 + 3x4 – x5) / 2x
x/2x + 2x2/2x + 3x4/2x – x5/2x
By using the formula an / am = an-m
1/2 x1-1 + x2-1 + 3/2 x4-1 – 1/2 x5-1
1/2 + x + 3/2 x3 – 1/2 x4
2. y4 – 3y3 + 1/2y2 by 3y
Solution:
We have,
(y4 – 3y3 + 1/2y2)/ 3y
y4/3y – 3y3/3y + (½)y2/3y
By using the formula an / am = an-m
1/3 y4-1 – y3-1 + 1/6 y2-1
1/3y3 – y2 + 1/6y
3. -4a3 + 4a2 + a by 2a
Solution:
We have,
(-4a3 + 4a2 + a) / 2a
-4a3/2a + 4a2/2a + a/2a
By using the formula an / am = an-m
-2a3-1 + 2a2-1 + 1/2 a1-1
-2a2 + 2a + ½
4. –x6 + 2x4 + 4x3 + 2x2 by √2x2
Solution:
We have,
(–x6 + 2x4 + 4x3 + 2x2) / √2x2
-x6/√2x2 + 2x4/√2x2 + 4x3/√2x2 + 2x2/√2x2
By using the formula an / am = an-m
-1/√2 x6-2 + 2/√2 x4-2 + 4/√2 x3-2 + 2/√2 x2-2
-1/√2 x4 + √2x2 + 2√2x + √2
5. -4a3 + 4a2 + a by 2a
Solution:
We have,
(-4a3 + 4a2 + a) / 2a
-4a3/2a + 4a2/2a + a/2a
By using the formula an / am = an-m
-2a3-1 + 2a2-1 + 1/2a1-1
-2a2 + 2a + ½
6. √3a4 + 2√3a3 + 3a2 – 6a by 3a
Solution:
We have,
(√3a4 + 2√3a3 + 3a2 – 6a) / 3a
√3a4/3a + 2√3a3/3a + 3a2/3a – 6a/3a
By using the formula an / am = an-m
√3/3 a4-1 + 2√3/3 a3-1 + a2-1 – 2a1-1
1/√3 a3 + 2/√3 a2 + a – 2
EXERCISE 8.4 PAGE NO: 8.11
Divide:
1. 5x3 – 15x2 + 25x by 5x
Solution:
We have,
(5x3 – 15x2 + 25x) / 5x
5x3/5x – 15x2/5x + 25x/5x
By using the formula an / am = an-m
5/5 x3-1 – 15/5 x2-1 + 25/5 x1-1
x2 – 3x + 5
2. 4z3 + 6z2 – z by -1/2z
Solution:
We have,
(4z3 + 6z2 – z) / -1/2z
4z3/(-1/2z) + 6z2/(-1/2z) – z/(-1/2z)
By using the formula an / am = an-m
-8 z3-1 – 12z2-1 + 2 z1-1
-8z2 – 12z + 2
3. 9x2y – 6xy + 12xy2 by -3/2xy
Solution:
We have,
(9x2y – 6xy + 12xy2) / -3/2xy
9x2y/(-3/2xy) – 6xy/(-3/2xy) + 12xy2/(-3/2xy)
By using the formula an / am = an-m
(-9×2)/3 x2-1y1-1 – (-6×2)/3 x1-1y1-1 + (-12×2)/3 x1-1y2-1
-6x + 4 – 8y
4. 3x3y2 + 2x2y + 15xy by 3xy
Solution:
We have,
(3x3y2 + 2x2y + 15xy) / 3xy
3x3y2/3xy + 2x2y/3xy + 15xy/3xy
By using the formula an / am = an-m
3/3 x3-1y2-1 + 2/3 x2-1y1-1 + 15/3 x1-1y1-1
x2y + 2/3x + 5
5. x3 + 7x + 12 by x + 4
Solution:
We have,
(x3 + 7x + 12) / (x + 4)
By using long division method
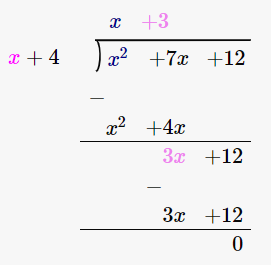
∴ (x3 + 7x + 12) / (x + 4) = x + 3
6. 4y2 + 3y + 1/2 by 2y + 1
Solution:
We have,
4y2 + 3y + 1/2 by (2y + 1)
By using long division method
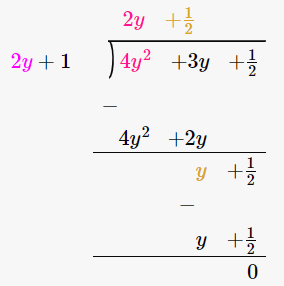
∴ (4y2 + 3y + 1/2) / (2y + 1) = 2y + 1/2
7. 3x3 + 4x2 + 5x + 18 by x + 2
Solution:
We have,
(3x3 + 4x2 + 5x + 18) / (x + 2)
By using long division method
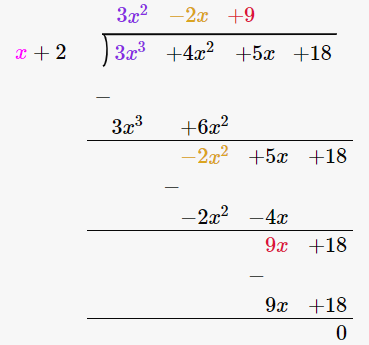
∴ (3x3 + 4x2 + 5x + 18) / (x + 2) = 3x2 – 2x + 9
8. 14x2 – 53x + 45 by 7x – 9
Solution:
We have,
(14x2 – 53x + 45) / (7x – 9)
By using long division method
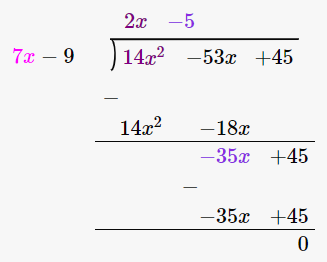
∴ (14x2 – 53x + 45) / (7x – 9) = 2x – 5
9. -21 + 71x – 31x2 – 24x3 by 3 – 8x
Solution:
We have,
-21 + 71x – 31x2 – 24x3 by 3 – 8x
(-24x3 – 31x2 + 71x – 21) / (3 – 8x)
By using long division method
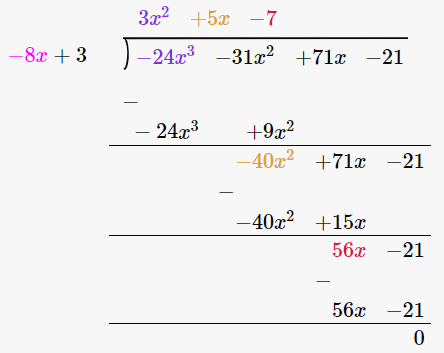
∴ (-24x3 – 31x2 + 71x – 21) / (3 – 8x) = 3x2 + 5x – 7
10. 3y4 – 3y3 – 4y2 – 4y by y2 – 2y
Solution:
We have,
(3y4 – 3y3 – 4y2 – 4y) / (y2 – 2y)
By using long division method
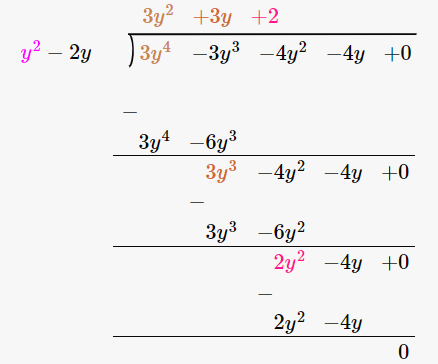
∴ (3y4 – 3y3 – 4y2 – 4y) / (y2 – 2y) = 3y2 + 3y + 2
11. 2y5 + 10y4 + 6y3 + y2 + 5y + 3 by 2y3 + 1
Solution:
We have,
(2y5 + 10y4 + 6y3 + y2 + 5y + 3) / (2y3 + 1)
By using long division method
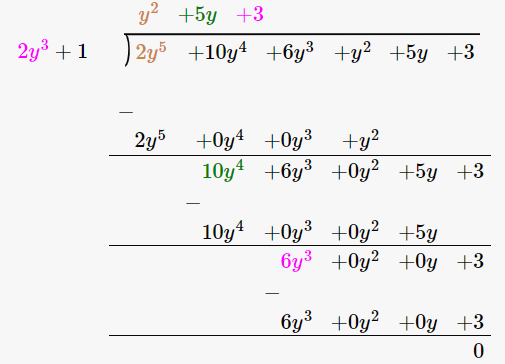
∴ (2y5 + 10y4 + 6y3 + y2 + 5y + 3) / (2y3 + 1) = y2 + 5y + 3
12. x4 – 2x3 + 2x2 + x + 4 by x2 + x + 1
Solution:
We have,
(x4 – 2x3 + 2x2 + x + 4) / (x2 + x + 1)
By using long division method
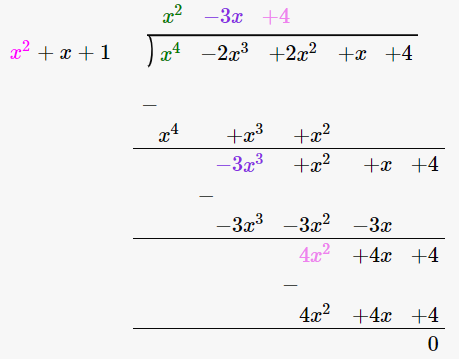
∴ (x4 – 2x3 + 2x2 + x + 4) / (x2 + x + 1) = x2 – 3x + 4
13. m3 – 14m2 + 37m – 26 by m2 – 12m + 13
Solution:
We have,
(m3 – 14m2 + 37m – 26) / (m2 – 12m + 13)
By using long division method
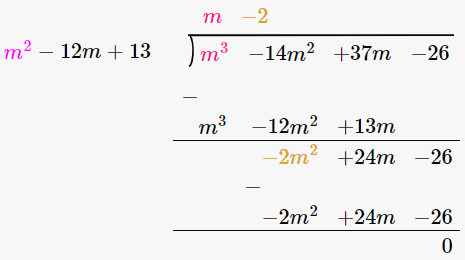
∴ (m3 – 14m2 + 37m – 26) / (m2 – 12m + 13) = m – 2
14. x4 + x2 + 1 by x2 + x + 1
Solution:
We have,
(x4 + x2 + 1) / (x2 + x + 1)
By using long division method
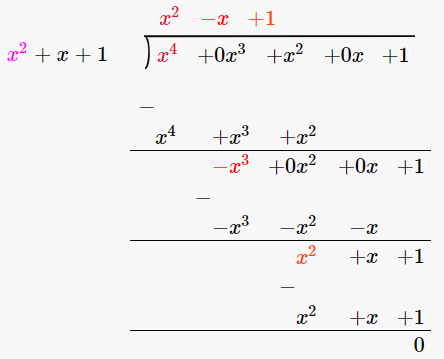
∴ (x4 + x2 + 1) / (x2 + x + 1) = x2 – x + 1
15. x5 + x4 + x3 + x2 + x + 1 by x3 + 1
Solution:
We have,
(x5 + x4 + x3 + x2 + x + 1) / (x3 + 1)
By using long division method
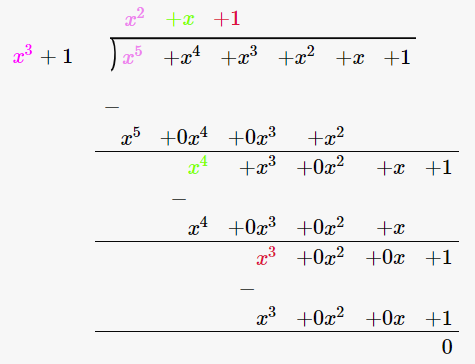
∴ (x5 + x4 + x3 + x2 + x + 1) / (x3 + 1) = x2 + x + 1
Divide each of the following and find the quotient and remainder:
16. 14x3 – 5x2 + 9x – 1 by 2x – 1
Solution:
We have,
(14x3 – 5x2 + 9x – 1) / (2x – 1)
By using long division method
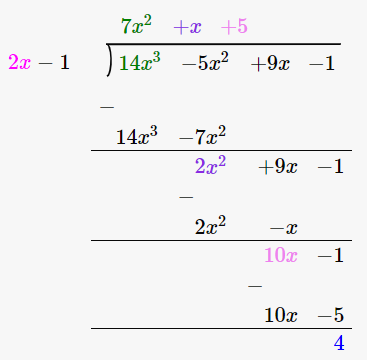
∴ Quotient is 7x2 + x + 5 and the Remainder is 4.
17. 6x3 – x2 – 10x – 3 by 2x – 3
Solution:
We have,
(6x3 – x2 – 10x – 3) / (2x – 3)
By using long division method
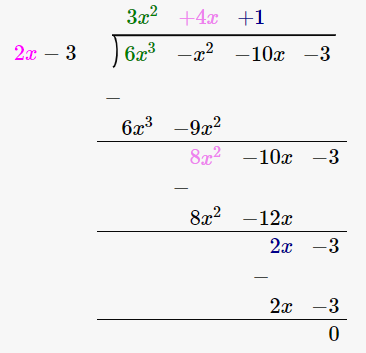
∴ Quotient is 3x2 + 4x + 1 and the Remainder is 0.
18. 6x3 + 11x2 – 39x – 65 by 3x2 + 13x + 13
Solution:
We have,
(6x3 + 11x2 – 39x – 65) / (3x2 + 13x + 13)
By using long division method
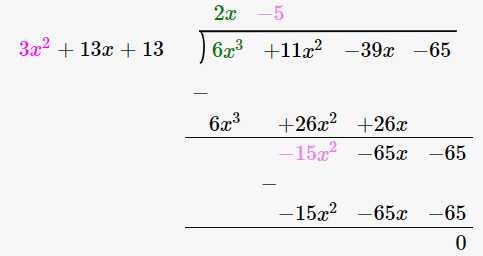
∴ Quotient is 2x – 5 and the Remainder is 0.
19. 30x4 + 11x3 – 82x2 – 12x + 48 by 3x2 + 2x – 4
Solution:
We have,
(30x4 + 11x3 – 82x2 – 12x + 48) / (3x2 + 2x – 4)
By using long division method
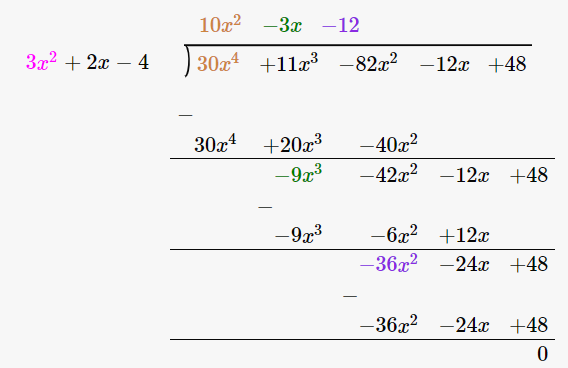
∴ Quotient is 10x2 – 3x – 12 and the Remainder is 0.
20. 9x4 – 4x2 + 4 by 3x2 – 4x + 2
Solution:
We have,
(9x4 – 4x2 + 4) / (3x2 – 4x + 2)
By using long division method
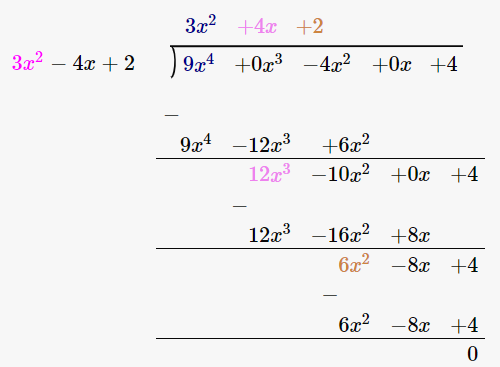
∴ Quotient is 3x2 + 4x + 2 and the Remainder is 0.
21. Verify division algorithm i.e. Dividend = Divisor × Quotient + Remainder, in each of the following. Also, write the quotient and remainder:
Dividend divisor
(i) 14x2 + 13x – 15 7x – 4
(ii) 15z3 – 20z2 + 13z – 12 3z – 6
(iii) 6y5 – 28y3 + 3y2 + 30y – 9 2x2 – 6
(iv) 34x – 22x3 – 12x4 – 10x2 – 75 3x + 7
(v) 15y4 – 16y3 + 9y2 – 10/3y + 6 3y – 2
(vi) 4y3 + 8y + 8y2 + 7 2y2 – y + 1
(vii) 6y4 + 4y4 + 4y3 + 7y2 + 27y + 6 2y3 + 1
Solution:
(i) Dividend divisor
14x2 + 13x – 15 7x – 4
By using long division method
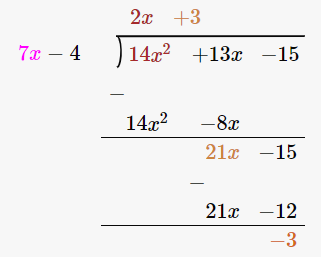
Let us verify, Dividend = Divisor × Quotient + Remainder
14x2 + 13x – 15 = (7x – 4) × (2x + 3) + (-3)
= 14x2 + 21x – 8x -12 -3
= 14x2 + 13x – 15
Hence, verified.
∴ Quotient is 2x + 3 and the Remainder is -3.
(ii) Dividend divisor
15z3 – 20z2 + 13z – 12 3z – 6
By using long division method
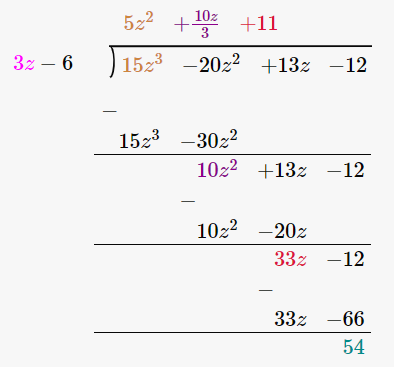
Let us verify, Dividend = Divisor × Quotient + Remainder
15z3 – 20z2 + 13z – 12 = (3z – 6) × (5z2 + 10z/3 + 11) + 54
= 15z3 + 10z2 + 33z – 30z2 – 20z + 54
= 15z2 – 20z2 + 13z – 12
Hence, verified.
∴ Quotient is 5z2 + 10z/3 + 11 and the Remainder is 54.
(iii) Dividend divisor
6y5 – 28y3 + 3y2 + 30y – 9 2x2 – 6
By using long division method
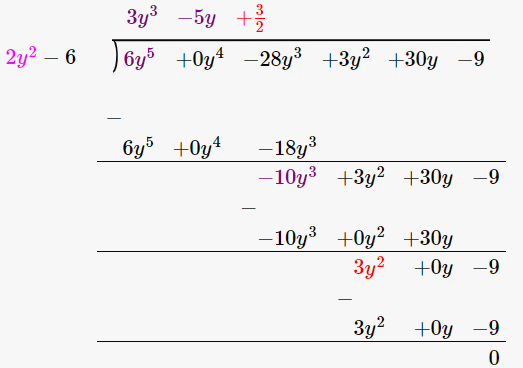
Let us verify, Dividend = Divisor × Quotient + Remainder
6y5 – 28y3 + 3y2 + 30y – 9 = (2x2 – 6) × (3y3 – 5y + 3/2) + 0
= 6y5 – 10y3 + 3y2 – 18y3 + 30y – 9
= 6y5 – 28y3 + 3y2 + 30y – 9
Hence, verified.
∴ Quotient is 3y3 – 5y + 3/2 and the Remainder is 0.
(iv) Dividend divisor
34x – 22x3 – 12x4 – 10x2 – 75 3x + 7
-12x4 – 22x3 – 10x2 + 34x – 75
By using long division method
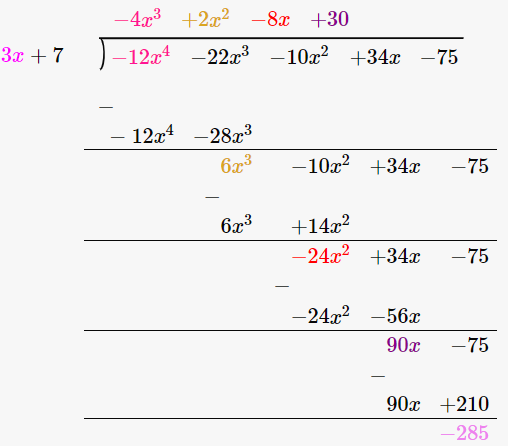
Let us verify, Dividend = Divisor × Quotient + Remainder
-12x4 – 22x3 – 10x2 + 34x – 75 = (3x + 7) × (-4x3 + 2x2 – 8x + 30) – 285
= -12x4 + 6x3 – 24x2 – 28x3 + 14x2 + 90x – 56x + 210 -285
= -12x4 – 22x3 – 10x2 + 34x – 75
Hence, verified.
∴ Quotient is -4x3 + 2x2 – 8x + 30 and the Remainder is -285.
(v) Dividend divisor
15y4 – 16y3 + 9y2 – 10/3y + 6 3y – 2
By using long division method
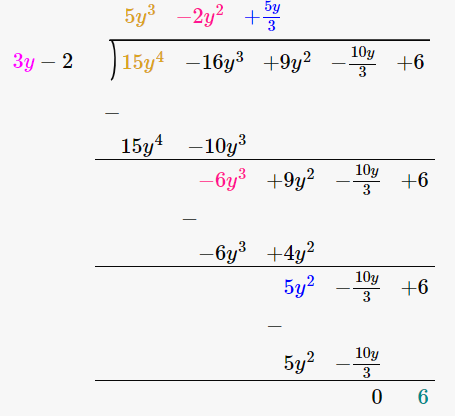
Let us verify, Dividend = Divisor × Quotient + Remainder
15y4 – 16y3 + 9y2 – 10/3y + 6 = (3y – 2) × (5y3 – 2y2 + 5y/3) + 6
= 15y4 – 6y3 + 5y2 – 10y3 + 4y2 – 10y/3 + 6
= 15y4 – 16y3 + 9y2 – 10/3y + 6
Hence, verified.
∴ Quotient is 5y3 – 2y2 + 5y/3 and the Remainder is 6.
(vi) Dividend divisor
4y3 + 8y + 8y2 + 7 2y2 – y + 1
4y3 + 8y2 + 8y + 7
By using long division method
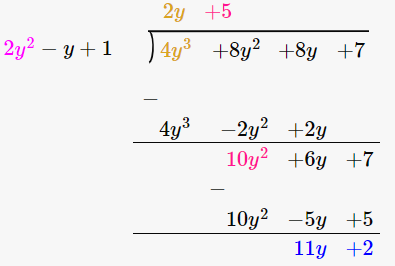
Let us verify, Dividend = Divisor × Quotient + Remainder
4y3 + 8y2 + 8y + 7 = (2y2 – y + 1) × (2y + 5) + 11y + 2
= 4y3 + 10y2 – 2y2 – 5y + 2y + 5 + 11y + 2
= 4y3 + 8y2 + 8y + 7
Hence, verified.
∴ Quotient is 2y + 5 and the Remainder is 11y + 2.
(vii) Dividend divisor
6y5 + 4y4 + 4y3 + 7y2 + 27y + 6 2y3 + 1
By using long division method
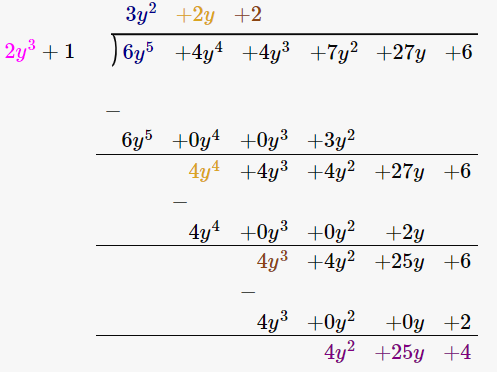
Let us verify, Dividend = Divisor × Quotient + Remainder
6y5 + 4y4 + 4y3 + 7y2 + 27y + 6 = (2y3 + 1) × (3y2 + 2y + 2) + 4y2 + 25y + 4
= 6y5 + 4y4 + 4y3 + 3y2 + 2y + 2 + 4y2 + 25y + 4
= 6y5 + 4y4 + 4y3 + 7y2 + 27y + 6
Hence, verified.
∴ Quotient is 3y2 + 2y + 2 and the Remainder is 4y2 + 25y + 4.
22. Divide 15y4+ 16y3 + 10/3y – 9y2 – 6 by 3y – 2 Write down the coefficients of the terms in the quotient.
Solution:
We have,
(15y4+ 16y3 + 10/3y – 9y2 – 6) / (3y – 2)
By using long division method
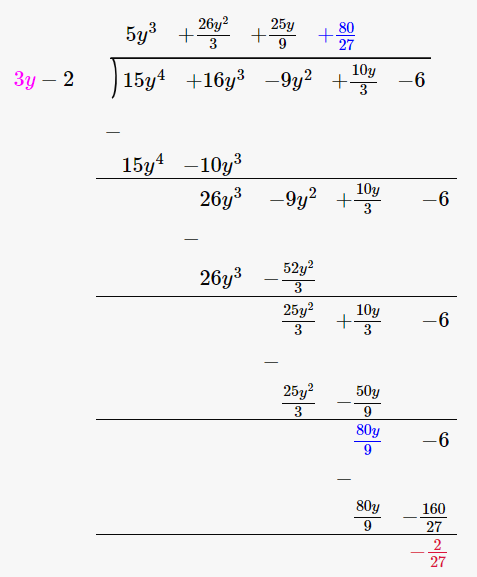
∴ Quotient is 5y3 + 26y2/3 + 25y/9 + 80/27
So the coefficients of the terms in the quotient are:
Coefficient of y3 = 5
Coefficient of y2 = 26/3
Coefficient of y = 25/9
Constant term = 80/27
23. Using division of polynomials state whether
(i) x + 6 is a factor of x2 – x – 42
(ii) 4x – 1 is a factor of 4x2 – 13x – 12
(iii) 2y – 5 is a factor of 4y4 – 10y3 – 10y2 + 30y – 15
(iv) 3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y – 35
(v) z2 + 3 is a factor of z5 – 9z
(vi) 2x2 – x + 3 is a factor of 6x5 – x4 + 4x3 – 5x2 – x – 15
(i) x + 6 is a factor of x2 – x – 42
(ii) 4x – 1 is a factor of 4x2 – 13x – 12
(iii) 2y – 5 is a factor of 4y4 – 10y3 – 10y2 + 30y – 15
(iv) 3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y – 35
(v) z2 + 3 is a factor of z5 – 9z
(vi) 2x2 – x + 3 is a factor of 6x5 – x4 + 4x3 – 5x2 – x – 15
Solution:
(i) x + 6 is a factor of x2 – x – 42
Firstly let us perform long division method
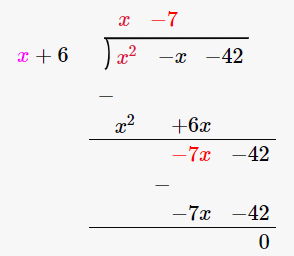
Since the remainder is 0, we can say that x + 6 is a factor of x2 – x – 42
(ii) 4x – 1 is a factor of 4x2 – 13x – 12
Firstly let us perform long division method
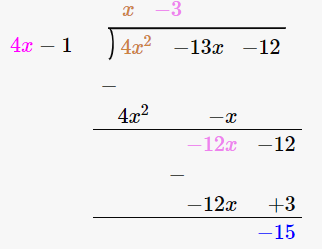
Since the remainder is -15, 4x – 1 is not a factor of 4x2 – 13x – 12
(iii) 2y – 5 is a factor of 4y4 – 10y3 – 10y2 + 30y – 15
Firstly let us perform long division method
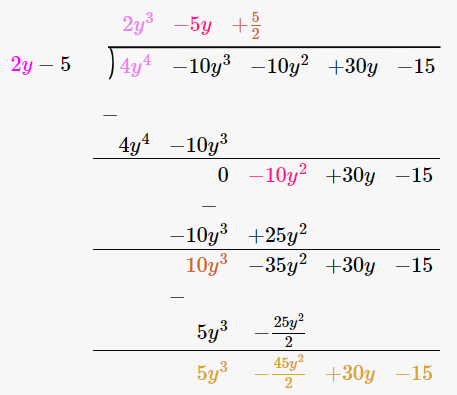
Since the remainder is 5y3 – 45y2/2 + 30y – 15, 2y – 5 is not a factor of 4y4 – 10y3 – 10y2 + 30y – 15
(iv) 3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y – 35
Firstly let us perform long division method
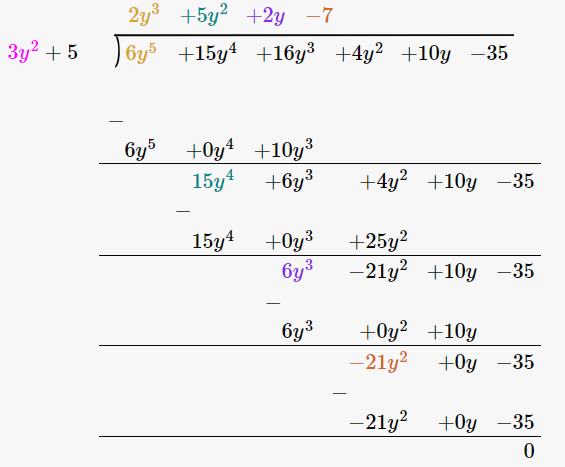
Since the remainder is 0, 3y2 + 5 is a factor of 6y5 + 15y4 + 16y3 + 4y2 + 10y – 35
(v) z2 + 3 is a factor of z5 – 9z
Firstly let us perform long division method
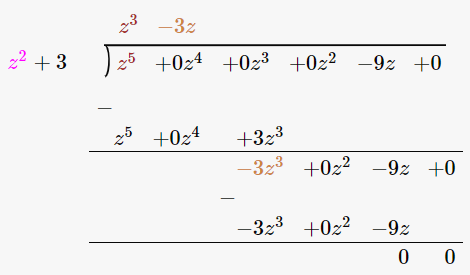
Since the remainder is 0, z2 + 3 is a factor of z5 – 9z
(vi) 2x2 – x + 3 is a factor of 6x5 – x4 + 4x3 – 5x2 – x – 15
Firstly let us perform long division method

Since the remainder is 0, 2x2 – x + 3 is a factor of 6x5 – x4 + 4x3 – 5x2 – x – 15
24. Find the value of a, if x + 2 is a factor of 4x4 + 2x3 – 3x2 + 8x + 5a
Solution:
We know that x + 2 is a factor of 4x4 + 2x3 – 3x2 + 8x + 5a
Let us equate x + 2 = 0
x = -2
Now let us substitute x = -2 in the equation 4x4 + 2x3 – 3x2 + 8x + 5a
4(-2)4 + 2(-2)3 – 3(-2)2 + 8(-2) + 5a = 0
64 – 16 – 12 – 16 + 5a = 0
20 + 5a = 0
5a = -20
a = -20/5
= -4
25. What must be added to x4 + 2x3 – 2x2 + x – 1 so that the resulting polynomial is exactly divisible by x2 + 2x -3.
Solution:
Firstly let us perform long division method
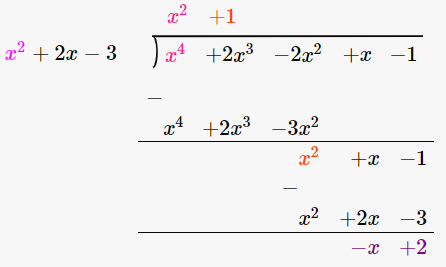
By long division method we got remainder as –x + 2,
∴ x – 2 has to be added to x4 + 2x3 – 2x2 + x – 1 so that the resulting polynomial is exactly divisible by x2 + 2x -3.
EXERCISE 8.5 PAGE NO: 8.15
1. Divide the first polynomial by the second polynomial in each of the following. Also, write the quotient and remainder:
(i) 3x2 + 4x + 5, x – 2
(ii) 10x2 – 7x + 8, 5x – 3
(iii) 5y3 – 6y2 + 6y – 1, 5y – 1
(iv) x4 – x3 + 5x, x – 1
(v) y4 + y2, y2 – 2
Solution:
(i) 3x2 + 4x + 5, x – 2
By using long division method
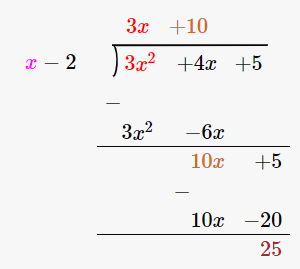
∴ the Quotient is 3x + 10 and the Remainder is 25.
(ii) 10x2 – 7x + 8, 5x – 3
By using long division method
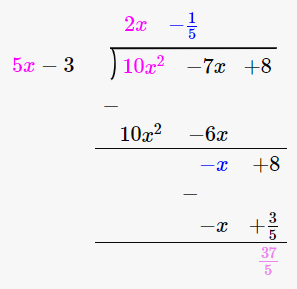
∴ the Quotient is 2x – 1/5 and the Remainder is 37/5.
(iii) 5y3 – 6y2 + 6y – 1, 5y – 1
By using long division method
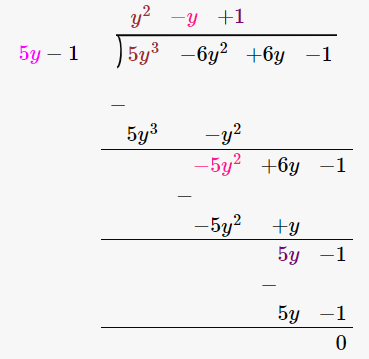
∴ the Quotient is y2 – y + 1 and the Remainder is 0.
(iv) x4 – x3 + 5x, x – 1
By using long division method
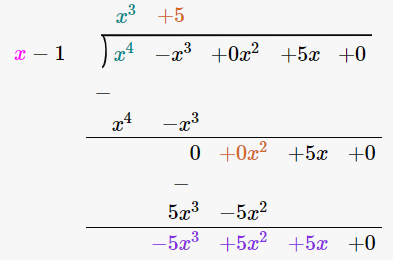
∴ the Quotient is x3 + 5 and the Remainder is 5.
(v) y4 + y2, y2 – 2
By using long division method
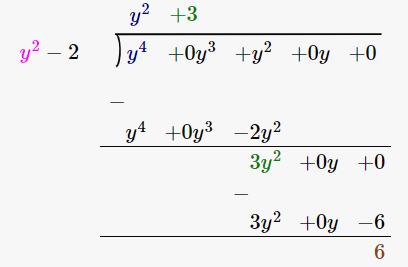
∴ the Quotient is y2 + 3 and the Remainder is 6.
2. Find Whether or not the first polynomial is a factor of the second:
(i) x + 1, 2x2 + 5x + 4
(ii) y – 2, 3y3 + 5y2 + 5y + 2
(iii) 4x2 – 5, 4x4 + 7x2 + 15
(iv) 4 – z, 3z2 – 13z + 4
(v) 2a – 3, 10a2 – 9a – 5
(vi) 4y + 1, 8y2 – 2y + 1
Solution:
(i) x + 1, 2x2 + 5x + 4
Let us perform long division method,
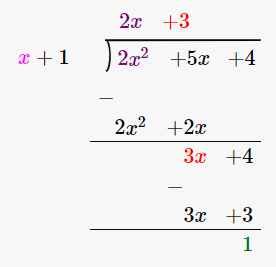
Since remainder is 1 therefore the first polynomial is not a factor of the second polynomial.
(ii) y – 2, 3y3 + 5y2 + 5y + 2
Let us perform long division method,
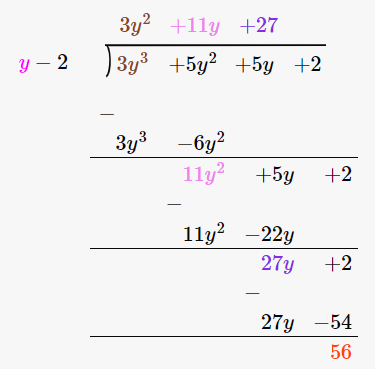
Since remainder is 56 therefore the first polynomial is not a factor of the second polynomial.
(iii) 4x2 – 5, 4x4 + 7x2 + 15
Let us perform long division method,
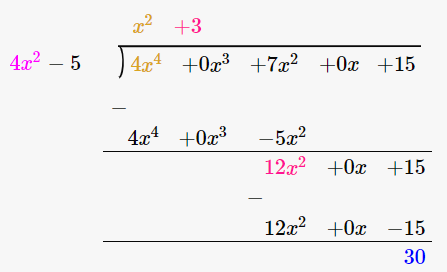
Since remainder is 30 therefore the first polynomial is not a factor of the second polynomial.
(iv) 4 – z, 3z2 – 13z + 4
Let us perform long division method,
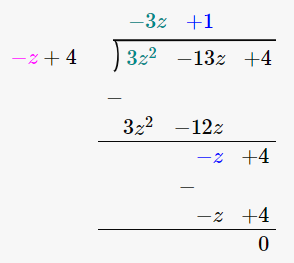
Since remainder is 0 therefore the first polynomial is a factor of the second polynomial.
(v) 2a – 3, 10a2 – 9a – 5
Let us perform long division method,
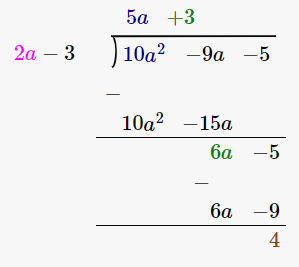
Since remainder is 4 therefore the first polynomial is not a factor of the second polynomial.
(vi) 4y + 1, 8y2 – 2y + 1
Let us perform long division method,
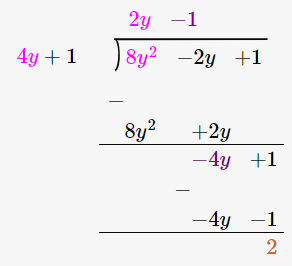
Since remainder is 2 therefore the first polynomial is not a factor of the second polynomial.
EXERCISE 8.6 PAGE NO: 8.17
Divide:
1. x2 – 5x + 6 by x – 3
Solution:
We have,
(x2 – 5x + 6) / (x – 3)
Let us perform long division method,
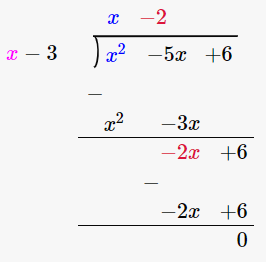
∴ the Quotient is x – 2
2. ax2 – ay2 by ax+ay
Solution:
We have,
(ax2 – ay2)/ (ax+ay)
(ax2 – ay2)/ (ax+ay) = (x – y) + 0/(ax+ay)
= (x – y)
∴ the answer is (x – y)
3. x4 – y4 by x2 – y2
Solution:
We have,
(x4 – y4)/ (x2 – y2)
(x4 – y4)/ (x2 – y2) = x2 + y2 + 0/(x2 – y2)
= x2 + y2
∴ the answer is (x2 + y2)
4. acx2 + (bc + ad)x + bd by (ax + b)
Solution:
We have,
(acx2 + (bc + ad) x + bd) / (ax + b)
(acx2 + (bc + ad) x + bd) / (ax + b) = cx + d + 0/ (ax + b)
= cx + d
∴ the answer is (cx + d)
5. (a2 + 2ab + b2) – (a2 + 2ac + c2) by 2a + b + c
Solution:
We have,
[(a2 + 2ab + b2) – (a2 + 2ac + c2)] / (2a + b + c)
= b – c
∴ the answer is (b – c)
6. 1/4x2 – 1/2x – 12 by 1/2x – 4
Solution:
We have,
(1/4x2 – 1/2x – 12) / (1/2x – 4)
Let us perform long division method,
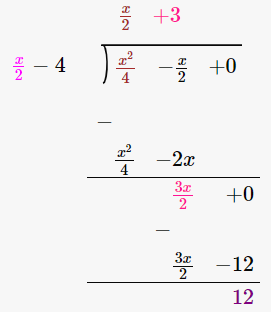
∴ the Quotient is x/2 + 3
