RD Sharma Solutions for Class 8 Chapter 19 Visualising Shapes Free Online
EXERCISE 19.1 PAGE NO: 19.9
1. What is the least number of planes that can enclose a solid? What is the name of the solid?
Solution:
The least number of planes that are required to enclose a solid is 4.
The name of solid is tetrahedron.
2. Can a polyhedron have for its faces?
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
(i) 3 triangles?
(ii) 4 triangles?
(iii) a square and four triangles?
Solution:
(i) 3 triangles?
No, because a polyhedron is a solid shape bounded by polygons.
(ii) 4 triangles?
Yes, because a tetrahedron as 4 triangles as its faces.
(iii) a square and four triangles?
Yes, because a square pyramid has a square and four triangles as its faces.
3. Is it possible to have a polyhedron with any given number of faces?
Solution:
Yes, if number of faces is four or more.
4. Is a square prism same as a cube?
Solution:
Yes. We know that a square is a three dimensional shape with six rectangular shaped sides, out of which two are squares. Cubes are of rectangular prism length, width and height of same measurement.
5. Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Solution:
No.
Let us use Euler’s formula
V + F = E + 2
15 + 10 = 20 + 2
25 ≠ 22
Since the given polyhedron is not following Euler’s formula, therefore it is not possible to have 10 faces, 20 edges and 15 vertices.
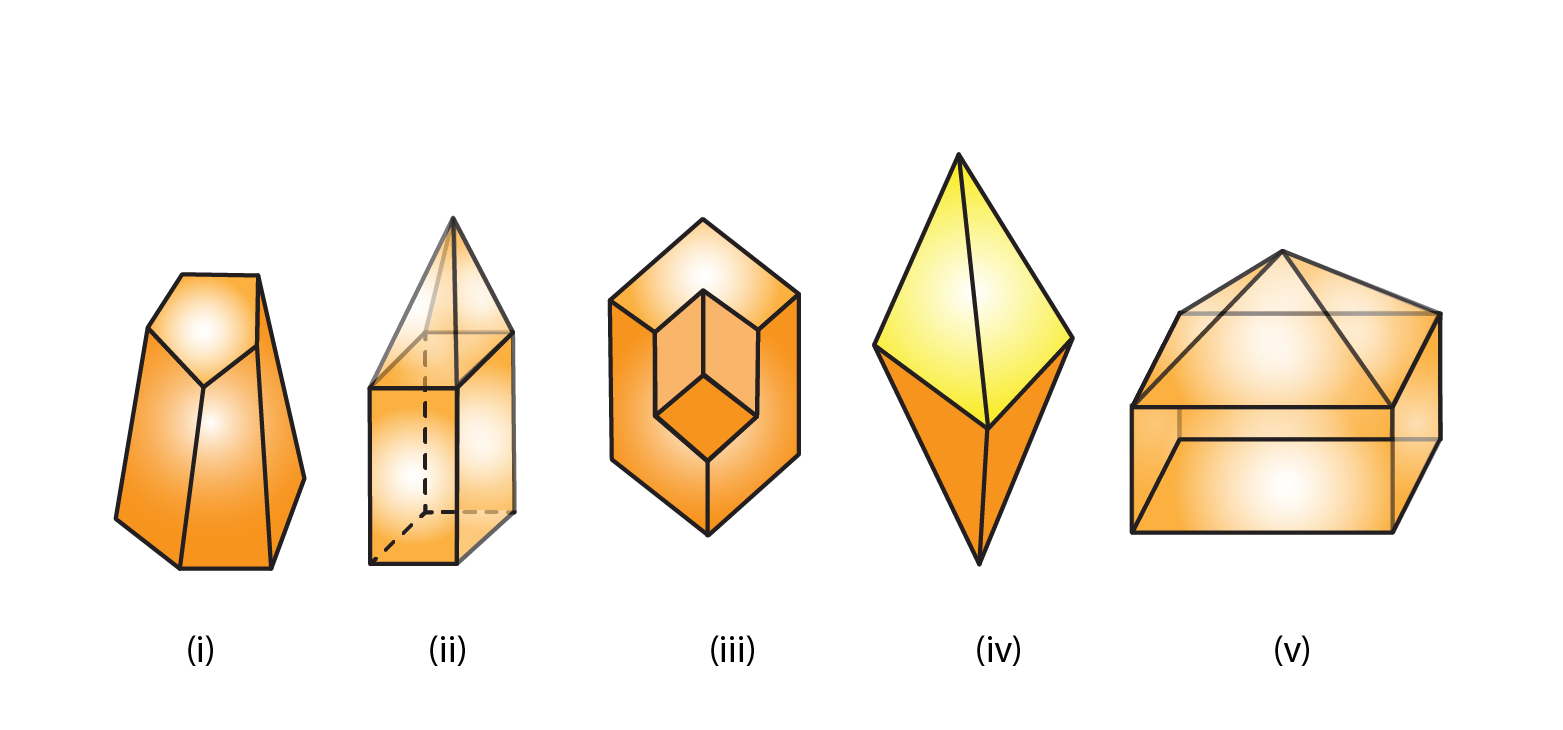
6. Verify Euler’s formula for each of the following polyhedrons:
Solution:
(i) Vertices = 10
Faces = 7
Edges = 15
By using Euler’s formula
V + F = E + 2
10 + 7 = 15 + 2
17 = 17
Hence verified.
(ii) Vertices = 9
Faces = 9
Edges = 16
By using Euler’s formula
V + F = E + 2
9 + 9 = 16 + 2
18 = 18
Hence verified.
(iii) Vertices = 14
Faces = 8
Edges = 20
By using Euler’s formula
V + F = E + 2
14 + 8 = 20 + 2
22 = 22
Hence verified.
(iv) Vertices = 6
Faces = 8
Edges = 12
By using Euler’s formula
V + F = E + 2
6 + 8 = 12 + 2
14 = 14
Hence verified.
(v) Vertices = 9
Faces = 9
Edges = 16
By using Euler’s formula
V + F = E + 2
9 + 9 = 16 + 2
18 = 18
Hence verified.
7. Using Euler’s formula find the unknown:
| Faces | ? | 5 | 20 |
| Vertices | 6 | ? | 12 |
| Edges | 12 | 9 | ? |
Solution:
(i)
By using Euler’s formula
V + F = E + 2
6 + F = 12 + 2
F = 14 – 6
F = 8
∴ Number of faces is 8
(ii)
By using Euler’s formula
V + F = E + 2
V + 5 = 9 + 2
V = 11 – 5
V = 6
∴ Number of vertices is 6
(iii)
By using Euler’s formula
V + F = E + 2
12 + 20 = E + 2
E = 32 – 2
E = 30
∴ Number of edges is 30
EXERCISE 19.2 PAGE NO: 19.12
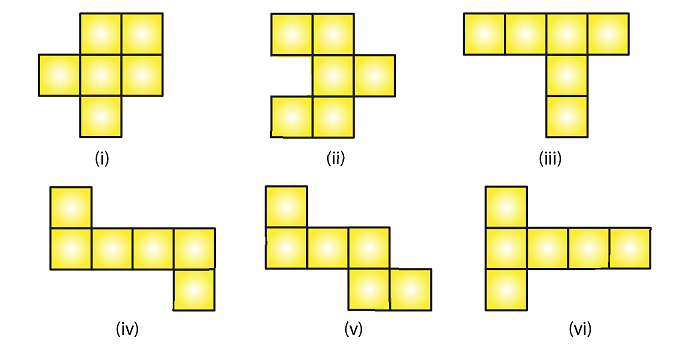
1. Which among of the following are nets for a cube?
Solution:
Figure (iv), (v), (vi) are the nets for a cube.
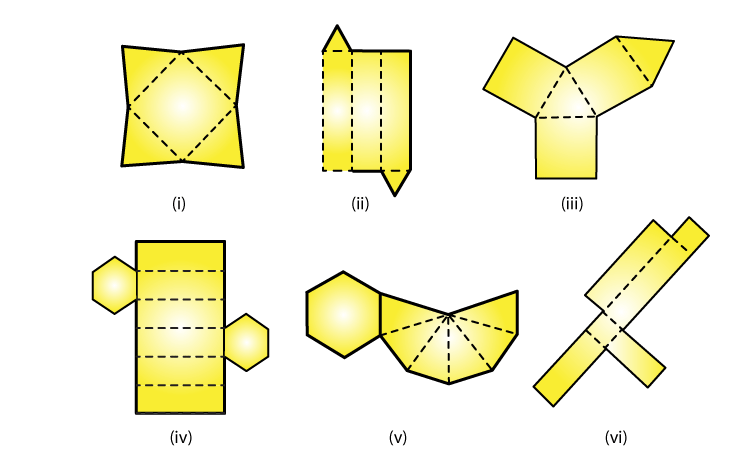
2. Name the polyhedron that can be made by folding each net:
Solution:
(i) From figure (i), a Square pyramid can be made by folding each net.
(ii) From figure (ii), a Triangular prism can be made by folding each net.
(iii) From figure (iii), a Triangular prism can be made by folding each net.
(iv) From figure (iv), a Hexagonal prism can be made by folding each net.
(iv) From figure (v), a Hexagonal pyramid can be made by folding each net.
(v) From figure (vi), a Cube can be made by folding each net.
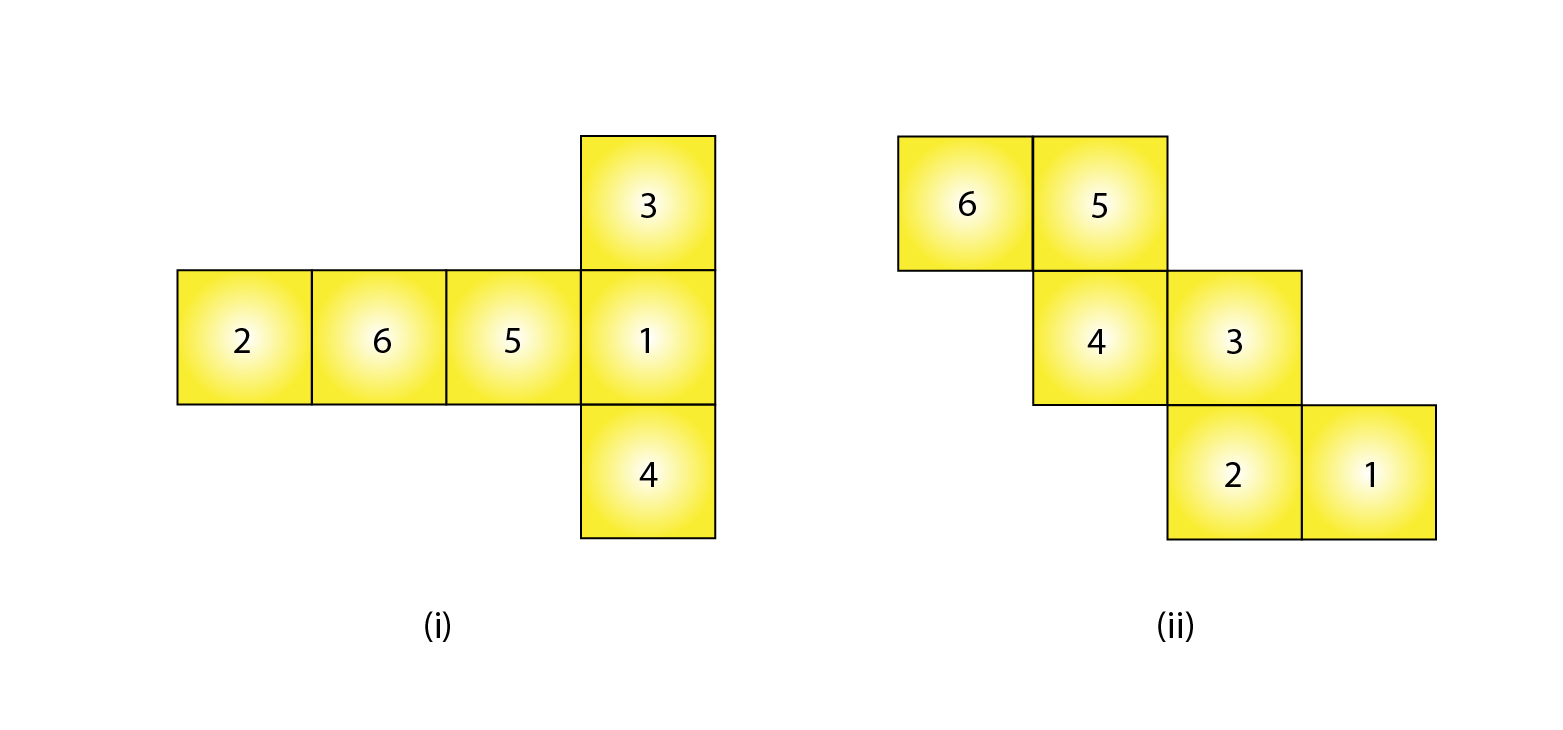
3. Dice are cubes where the numbers on the opposite faces must total 7. Which of the following are dice?
Solution:
Figure (i), is a dice. Since the sum of numbers on opposite faces is 7 (3 + 4 = 7 and 6 + 1 = 7).
4. Draw nets for each of the following polyhedrons:
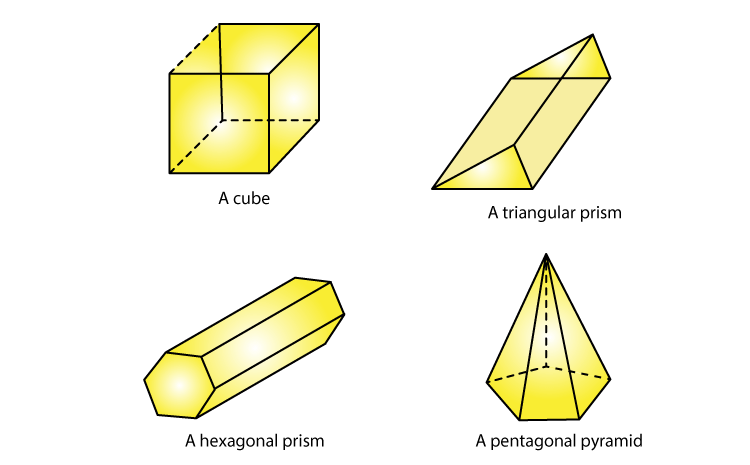
Solution:
(i) The net pattern for cube is

(ii) The pattern for triangular prism is
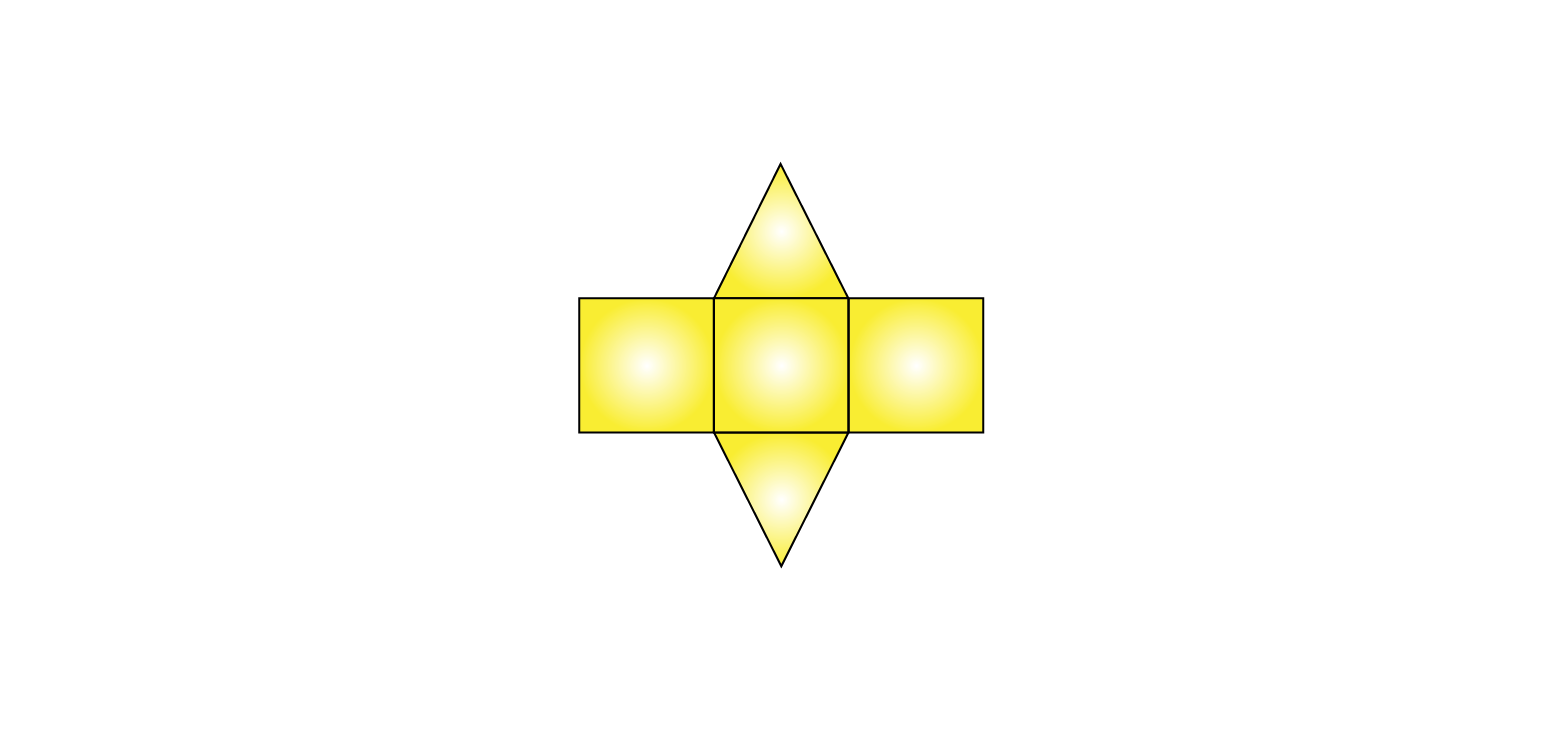
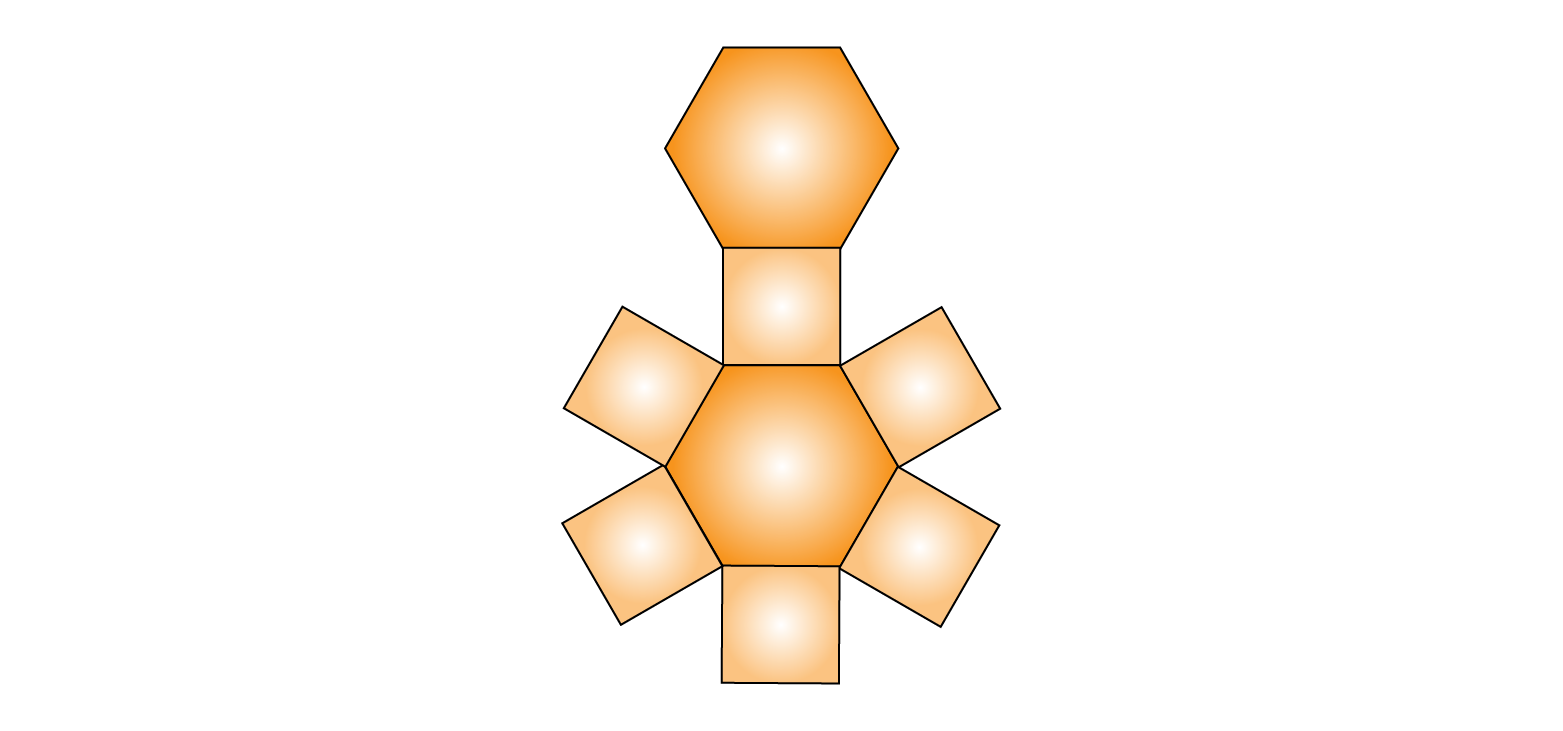
(iii) The net pattern for hexagonal prism is
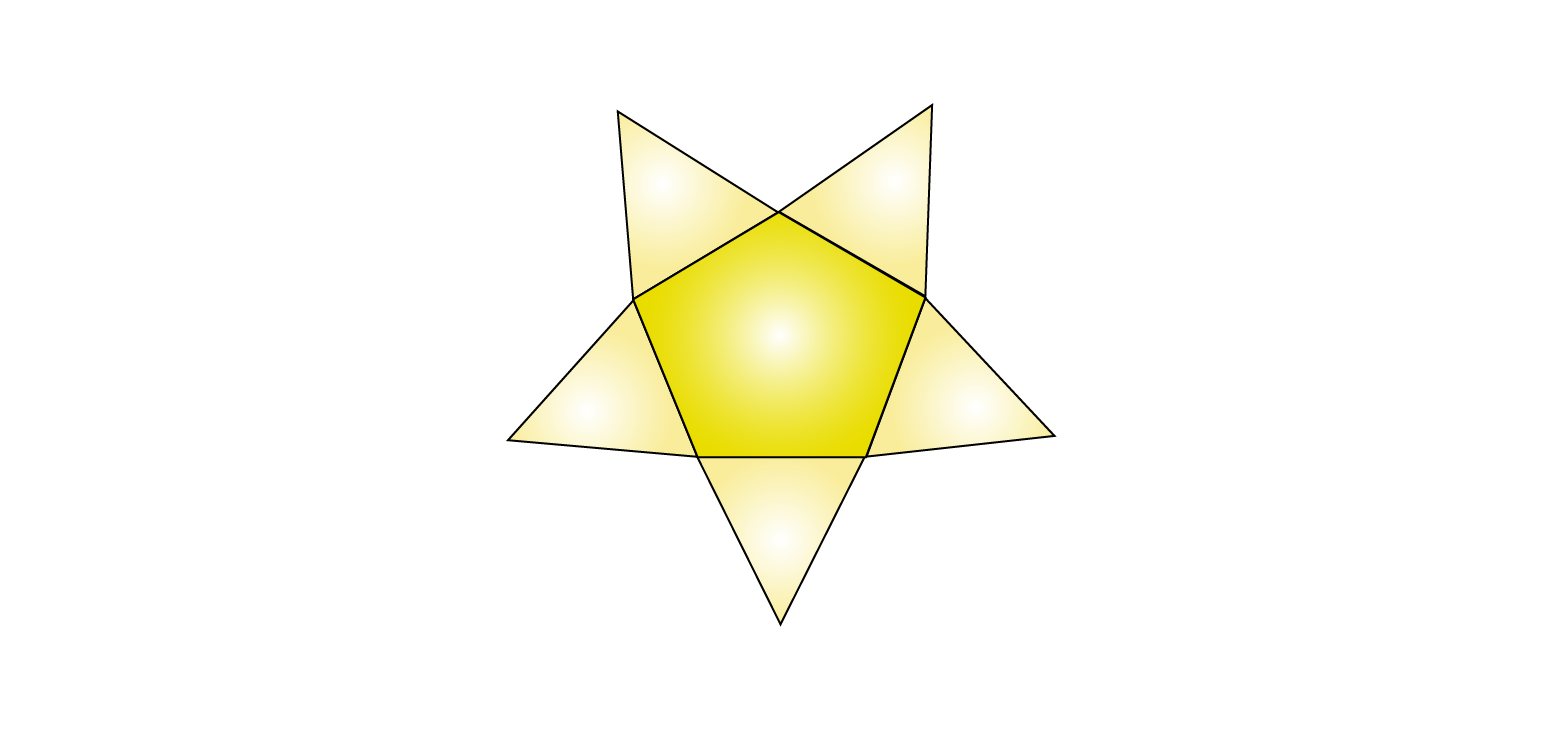
(iv) The net pattern for pentagonal pyramid is
5. Match the following figures:
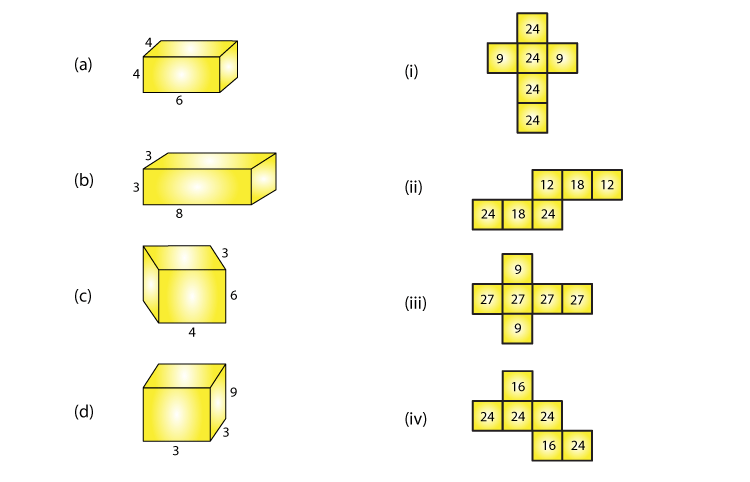
Solution:
(a)-(iv) Because multiplication of numbers on adjacent faces are equal, where 6×4 = 24 and 4×4 = 16
(b)-(i) Because multiplication of numbers on adjacent faces are equal, where 3×3 = 9 and 8×3 = 24
(c)-(ii) Because multiplication of numbers on adjacent faces are equal, where 6×4 = 24 and 6×3 = 18
(d)-(iii) Because multiplication of numbers on adjacent faces are equal, where 3×3 = 9 and 3×9 = 27
