RD Sharma Solutions for Class 6 Chapter 5 Negative Numbers and Integers

RD Sharma Solutions for Class 6 Chapter 5 Negative Numbers and Integers Free Online

Exercise 5.1 PAGE: 5.5

1. Write the opposite of each of the following:

(i) Increase in population

(ii) Depositing money in a bank

(iii) Earning money

(iv) Going North

(v) Gaining a weight of 4kg

(vi) A loss of Rs 1000

(vii) 25

(viii) – 15

Solution:

(i) The opposite of Increase in population is Decrease in population.

(ii) The opposite of Depositing money in a bank is Withdrawing money from a bank.

(iii) The opposite of earning money is Spending money.

(iv) The opposite of Going North is Going South.

(v) The opposite of gaining a weight of 4kg is losing a weight of 4kg.

(vi) The opposite of a loss of Rs 1000 is a gain of Rs 1000.

(vii) The opposite of 25 is – 25.

(viii) The opposite of – 15 is 15.

2. Indicate the following by using integers:

(i) 25o above zero

(ii) 5o below zero

(iii) A profit of Rs 800

(iv) A deposit of Rs 2500

(v) 3km above sea level

(vi) 2km below level

Solution:

(i) 25o above zero is + 25o.

(ii) 5o below zero is – 5o.

(iii) A profit of Rs 800 is + 800.

(iv) A deposit of Rs 2500 is + 2500.

(v) 3km above sea level is + 3.

(vi) 2km below level is – 2.

3. Mark the following integers on a number line:

(i) 7

(ii) -4

(iii) 0

Solution:

The following integers are marked on a number line as given below:

4. Which number in each of the following pairs is smaller?

(i) 0, -4

(ii) -3 , 12

(iii) 8, 13

(iv) – 15, -27

Solution:

(i) 0 is greater than the negative integers

So we get – 4 < 0

Therefore, – 4 is smaller.

(ii) 12 is greater than -3 on a number line

So we get

-3 < 12

Therefore, – 3 is smaller.

(iii) 13 is greater than 8 on a number line

So we get 8 < 13

Therefore, 8 is smaller.

(iv) – 15 is greater than – 27 on a number line

So we get – 27 < – 15

Therefore, – 27 is smaller.

5. Which number in each of the following pairs is larger?

(i) 3, -4

(ii) – 12, – 8

(iii) 0, 7

(iv) 12, – 18

Solution:

(i) We know that 3 is larger than – 4 on a number line

So we get 3 > – 4

Therefore, 3 is larger.

(ii) We know that – 8 is larger than – 12 on a number line

So we get – 8 > – 12

Therefore, – 8 is larger.

(iii) We know that 7 is larger than 0 on a number line

So we get 7 > 0

Therefore, 7 is larger.

(iv) We know that 12 is larger than – 18 on a number line

So we get 12 > – 18

Therefore, 12 is larger.

6. Write all integers between:

(i) – 7 and 3

(ii) – 2 and 2

(iii) – 4 and 0

(iv) 0 and 3

Solution:

(i) The integers between – 7 and 3 are

– 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2

(ii) The integers between – 2 and 2 are

-1, 0, 1.

(iii) The integers between – 4 and 0 are

-3, -2, -1

(iv) The integers between 0 and 3 are

1, 2.

7. How many integers are between?

(i) – 4 and 3

(ii) 5 and 12

(iii) – 9 and – 2

(iv) 0 and 5

Solution:

(i) The integers between – 4 and 3 are

-3, -2, -1, 0, 1, 2

Therefore, number of integers between – 4 and 3 are 6.

(ii) The integers between 5 and 12 are

6, 7, 8, 9, 10, 11

Therefore, number of integers between 5 and 12 are 6.

(iii) The integers between – 9 and – 2 are

-8, -7, -6, -5, -4, -3

Therefore, number of integers between -9 and -2 are 6.

(iv) The integers between 0 and 5 are

1, 2, 3, 4

Therefore, number of integers between 0 and 5 are 4.

8. Replace * in each of the following by < or > so that the statement is true:

(i) 2 * 5

(ii) 0 * 3

(iii) 0 * – 7

(iv) – 18 * 15

(v) – 235 * – 532

(vi) – 20 * 20

Solution:

(i) 2 < 5

(ii) 0 < 3

(iii) 0 > – 7

(iv) – 18 < 15

(v) – 235 > – 532

(vi) – 20 < 20

9. Write the following integers in increasing order:

(i) – 8, 5, 0, -12, 1, -9, 15

(ii) – 106, 107, – 320, – 7, 185

Solution:

(i) – 8, 5, 0, -12, 1, -9, 15 can be written in increasing order as

– 12, – 9, – 8, 0, 1, 5, 15

(ii) – 106, 107, – 320, – 7, 185 can be written in increasing order as

-320, – 106, – 7, 107, 185.

10. Write the following integers in decreasing order:

(i) – 15, 0, -2, -9, 7, 6, -5, 8

(ii) -154, 123, -205, -89, -74

Solution:

(i) – 15, 0, -2, -9, 7, 6, -5, 8 can be written in decreasing order as

8, 7, 6, 0, -2, -5, -9, -15

(ii) -154, 123, -205, -89, -74 can be written in decreasing order as

123, – 74, – 89, – 154, – 205

11. Using the number line, write the integer which is:

(i) 2 more than 3

(ii) 5 less than 3

(iii) 4 more than – 9

Solution:

(i) 2 more than 3

In order to get the integer 2 more than 3

We draw a number line from 3 and proceed 2 units to the right to obtain 5

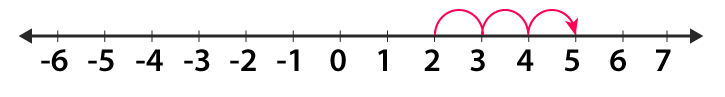
Therefore, 2 more than 3 is 5.

(ii) 5 less than 3

In order to get the integer 5 less than 3

We draw a number line from 3 and proceed 5 units to the left to obtain – 2

Therefore, 5 less than 3 is – 2.

(iii) 4 more than – 9

In order to get the integer 4 more than – 9

We draw a number line from – 9 and proceed 4 units to the right to obtain -5

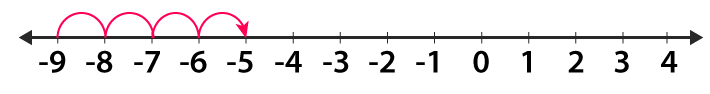
Therefore, 4 more than – 9 is – 5.

12. Write the absolute value of each of the following:

(i) 14

(ii) – 25

(iii) 0

(iv) – 125

(v) – 248

(vi) a – 7, if a is greater than 7

(vii) a – 7, if a – 2 is less than 7

(viii) a + 4, if a is greater than -4

(ix) a + 4 if a is less than – 4

(x) |-3|

(xi) -|-5|

(xii) |12 – 5|

Solution:

(i) The absolute value of 14 is

|14| = 14

(ii) The absolute value of – 25 is

|-25| = 25

(iii) The absolute value of 0 is

|0| = 0

(iv) The absolute value of – 125 is

|-125| = 125

(v) The absolute value of – 248 is

|-248| = 248

(vi) The absolute value of a – 7, if a is greater than 7 is

|a – 7| = a – 7 where a > 7

(vii) The absolute value of a – 7, if a – 2 is less than 7 is

|a – 7| = – (a – 7) where a – 2 < 7

(viii) The absolute value of a + 4, if a is greater than -4 is

|a + 4| = a + 4 where a > – 4

(ix) The absolute value of a + 4 if a is less than – 4 is

|a + 4| = – (a + 4) where a < -4

(x) The absolute value of |-3| is

|-3| = 3

(xi) The absolute value of -|-5| is

-|-5| = 5

(xii) The absolute value of |12 – 5| is

|12 – 5| = 7

13. (i) Write 4 negative integers less than – 10.

(ii) Write 6 negative integers just greater than – 12.

Solution:

(i) The 4 negative integers less than – 10 are

– 11, – 12, – 13, – 14

(ii) The 6 negative integers just greater than – 12 are

-11, – 10, – 9, – 8, – 7, – 6

14. Which of the following statements are true?

(i) The smallest integer is zero.

(ii) The opposite of zero is zero.

(iii) Zero is not an integer.

(iv) 0 is larger than every negative integer.

(v) The absolute value of an integer is greater than the integer.

(vi) A positive integer is greater than its opposite.

(vii) Every negative integer is less than every natural number.

(viii) 0 is the smallest positive integer.

Solution:

(i) False. The smallest integer is 1.

(ii) True. 0 is neither positive nor negative so the opposite is 0.

(iii) False. Zero is an integer which is neither positive nor negative.

(iv) True. 0 is larger than – 1.

(v) False. The absolute value of an integer is the numerical value.

(vi) True. 3 is greater than – 3.

(vii) True. – 3 is less than 1.

(viii) False. 1 is the smallest positive integer.

---

Exercise 5.2 PAGE: 5.9

1. Draw a number line and represent each of the following on it:

(i) 5 + (-2)

(ii) (-9) + 4

(iii) (-3) + (-5)

(iv) 6 + (-6)

(v) (-1) + (-2) + 2

(vi) (-2) + 7 + (-9)

Solution:

(i) 5 + (-2)

From 0 move towards right of first five units to obtain + 5

So the second number is – 2 so move 2 units towards left of + 5 we get + 3

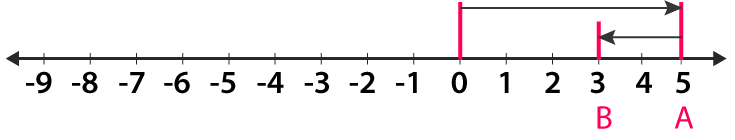
Therefore, 5 + (-2) = 3.

(ii) (-9) + 4

From 0 move towards left of nine units to obtain – 9

So the second number is 4 so move 4 units towards right of – 9 we get – 5

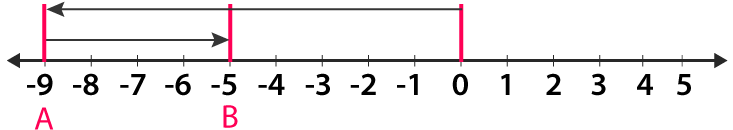
Therefore, (-9) + 4 = – 5.

(iii) (-3) + (-5)

From 0 move towards left of three units to obtain – 3

So the second number is – 5 so move 5 units towards left of – 3 we get – 8

Therefore, (-3) + (-5) = – 8.

(iv) 6 + (-6)

From zero move towards right of six units to obtain 6

So the second number is – 6 so move 6 units towards left of 6 we get 0

Therefore, 6 + (-6) = 0.

(v) (-1) + (-2) + 2

From zero move towards left of one unit to obtain – 1

So the second number is – 2 so move 2 units towards left of – 1 we get – 3

The third number is 2 so move 2 units towards right of – 3 we get – 1

Therefore, (-1) + (-2) + 2 = – 1.

(vi) (-2) + 7 + (-9)

From zero move towards left of two units to obtain – 2

So the second number is 7 so move 7 units towards right of – 2 we get 5

The third number is – 9 so move 9 units towards left of 5 we get – 4

Therefore, (-2) + 7 + (-9) = – 4.

2. Find the sum of

(i) -557 and 488

(ii) -522 and -160

(iii) 2567 and – 325

(iv) -10025 and 139

(v) 2547 and -2548

(vi) 2884 and -2884

Solution:

(i) -557 and 488

We get

-557 + 488

It can be written as

|-557| – |488| = 557 – 488 = – 69.

(ii) -522 and -160

We get

-522 + (-160)

It can be written as

-522 – 160 = – 682

(iii) 2567 and – 325

We get

2567 + (-325)

It can be written as

2567 – 325 = 2242

(iv) -10025 and 139

We get

-10025 + 139

It can be written as

-10025 + 139 = -9886

(v) 2547 and -2548

We get

2547 + (-2548)

It can be written as

2547 – 2548 = -1

(vi) 2884 and -2884

We get

2884 + (-2884)

It can be written as

2884 – 2884 = 0

---

Exercise 5.3 page: 5.11

1. Find the additive inverse of each of the following integers:

(i) 52

(ii) – 176

(iii) 0

(iv) 1

Solution:

(i) The additive inverse of 52 is – 52.

(ii) The additive inverse of – 176 is 176.

(iii) The additive inverse of 0 is 0.

(iv) The additive inverse of 1 is – 1.

2. Find the successor of each of the following integers:

(i) – 42

(ii) -1

(iii) 0

(iv) – 200

(v) -99

Solution:

(i) The successor of – 42 = – 42 + (-1)

We get

= 1 – 42 = – 41

(ii) The successor of – 1 is

-1 + 1 = 0

(iii) The successor of 0 is

0 + 1 = 1

(iv) The successor of – 200 is

-200 + 1 = – 199

(v) The successor of – 99 is

– 99 + 1 = – 98

3. Find the predecessor of each of the following integers:

(i) 0

(ii) 1

(iii) – 1

(iv) – 125

(v) 1000

Solution:

(i) The predecessor of 0 is

0 – 1 = – 1

(ii) The predecessor of 1 is

1 – 1 = 0

(iii) The predecessor of -1 is

-1 – 1 = -2

(iv) The predecessor of – 125 is

-125 – 1 = – 126

(v) The predecessor of 1000 is

1000 – 1 = 999

4. Which of the following statements are true?

(i) The sum of a number and its opposite is zero.

(ii) The sum of two negative integers is a positive integer.

(iii) The sum of a negative integer and a positive integer is always a negative integer.

(iv) The successor of – 1 is 1.

(v) The sum of three different integers can never be zero.

Solution:

(i) True. 1 – 1 = 0

(ii) False. -1 – 1 = -2

(iii) False. – 2 + 3 = 1

(iv) False. The successor of – 1 is 0.

(v) False. 1 + 2 – 3 = 0

5. Write all integers whose absolute values are less than 5.

Solution:

The integers whose absolute values are less than 5 are

-4, – 3, – 2, – 1, 0, 1, 2, 3, 4

6. Which of the following is false:

(i) |4 + 2| = |4| + |2|

(ii) |2 – 4| = |2| + |4|

(iii) |4 – 2| = |4| – |2|

(iv) |(-2) + (-4)| = |-2| + |-4|

Solution:

(i) True.

(ii) False.

(iii) True.

(iv) True.

7. Complete the following table:

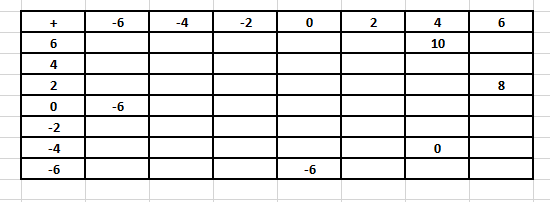
From the above table:

(i) Write all the pairs of integers whose sum is 0.

(ii) Is (-4) + (-2) = (-2) + (-4)?

(iii) Is 0 + (-6) = -6?

Solution:

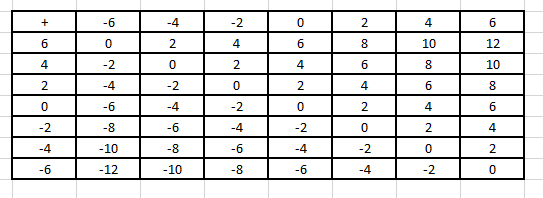
(i) The pairs of integers whose sum is 0 are

(6, -6), (4, – 4), (3, – 3), (2, – 2), (1, – 1), (0, 0)

(ii) Yes. By using commutativity of addition (-4) + (-2) = (-2) + (-4)

(iii) Yes. By using additive identity 0 + (-6) = -6.

8. Find an integer x such that

(i) x + 1 = 0

(ii) x + 5 = 0

(iii) – 3 + x = 0

(iv) x + (-8) = 0

(v) 7 + x = 0

(vi) x + 0 = 0

Solution:

(i) x + 1 = 0

Subtracting 1 on both sides

x + 1 – 1 = 0 – 1

We get

x = -1

(ii) x + 5 = 0

By subtracting 5 on both sides

x + 5 – 5 = 0 – 5

So we get

x = -5

(iii) – 3 + x = 0

By adding 3 on both sides

-3 + x + 3 = 0 + 3

So we get

x = 3

(iv) x + (-8) = 0

By adding 8 on both sides

x – 8 + 8 = 0 + 8

So we get

x = 8

(v) 7 + x = 0

By subtracting 7 on both sides

7 + x – 7 = 0 – 7

So we get

x = – 7

(vi) x + 0 = 0

So we get

x = 0

---

Exercise 5.4 page: 5.17

1. Subtract the first integer from the second in each of the following:

(i) 12, -5

(ii) – 12, 8

(iii) – 225, – 135

(iv) 1001, 101

(v) – 812, 3126

(vi) 7560, – 8

(vii) – 3978, – 4109

(viii) 0, – 1005

Solution:

(i) 12, -5

So by subtracting the first integer from the second

-5 – 12 = – 17

(ii) – 12, 8

So by subtracting the first integer from the second

8 – (-12) = 8 + 12 = 20

(iii) – 225, – 135

So by subtracting the first integer from the second

-135 – (-225) = 225 – 135 = 90

(iv) 1001, 101

So by subtracting the first integer from the second

101 – 1001 = – 900

(v) – 812, 3126

So by subtracting the first integer from the second

3126 – (-812) = 3126 + 812 = 3938

(vi) 7560, – 8

So by subtracting the first integer from the second

-8 – 7560 = – 7568

(vii) – 3978, – 4109

So by subtracting the first integer from the second

-4109 – (-3978) = – 4109 + 3978 = -131

(viii) 0, – 1005

So by subtracting the first integer from the second

-1005 – 0 = – 1005

2. Find the value of:

(i) – 27 – (- 23)

(ii) – 17 – 18 – (-35)

(iii) – 12 – (-5) – (-125) + 270

(iv) 373 + (-245) + (-373) + 145 + 3000

(v) 1 + (-475) + (-475) + (-475) + (-475) + 1900

(vi) (-1) + (-304) + 304 + 304 + (-304) + 1

Solution:

(i) – 27 – (- 23)

So we get

= – 27 + 23

On further calculation

= 23 – 27

We get

= – 4

(ii) – 17 – 18 – (-35)

So we get

= – 35 + 35

On further calculation

= 0

(iii) – 12 – (-5) – (-125) + 270

So we get

= – 12 + 5 + 125 + 270

On further calculation

= 400 – 12

We get

= 388

(iv) 373 + (-245) + (-373) + 145 + 3000

So we get

= 373 – 245 – 373 + 145 + 3000

On further calculation

= 3145 + 373 – 373 – 245

We get

= 3145 – 245

By subtraction

= 2900

(v) 1 + (-475) + (-475) + (-475) + (-475) + 1900

So we get

= 1 – 950 – 950 + 1900

On further calculation

= 1900 + 1 – 1900

We get

= 1

(vi) (-1) + (-304) + 304 + 304 + (-304) + 1

So we get

= – 1 + 1 – 304 + 304 – 304 + 304

On further calculation

= 0

3. Subtract the sum of – 5020 and 2320 from – 709.

Solution:

We know that the sum of 5020 and 2320 is

-5020 + 2320

It can be written as

= 2320 – 5020

So we get

= – 2700

Subtracting – 709 we get

= – (-2700) + (-709)

On further calculation

= – 709 – (-2700)

We get

= – 709 + 2700

By subtraction

= 1991

4. Subtract the sum of – 1250 and 1138 from the sum of 1136 and – 1272.

Solution:

We know that the sum of – 1250 and 1138 is

-1250 + 1138

It can be written as

= 1138 – 1250

So we get

= – 112

We know that the sum of 1136 and – 1272 is

1136 – 1272 = – 136

So we get

-136 – (-112) = – 136 + 112 = -24

5. From the sum of 233 and – 147, subtract – 284.

Solution:

We know that the sum of 233 and – 147 is

233 – 147 = 86

Subtracting – 284 we get

86 – (-284) = 86 + 284 = 370

6. The sum of two integers is 238. If one of the integers is – 122, determine the other.

Solution:

It is given that

Sum of two integers = 238

One of the integers = – 122

So the other integer = – (-122) + 138

On further calculation

Other integer = 238 + 122 = 360

7. The sum of two integers is – 223. If one of the integers is 172, find the other.

Solution:

It is given that

Sum of two integers = – 223

One of the integers = 172

So the other integer = – 223 – 172 = – 395

8. Evaluate the following:

(i) – 8 – 24 + 31 – 26 – 28 + 7 + 19 – 18 – 8 + 33

(ii) – 26 – 20 + 33 – (-33) + 21 + 24 – (-25) – 26 – 14 – 34

Solution:

(i) – 8 – 24 + 31 – 26 – 28 + 7 + 19 – 18 – 8 + 33

We get

= – 8 – 24 – 26 – 28 – 18 – 8 + 31 + 7 + 19 + 33

On further calculation

= – 32 – 26 – 28 – 26 + 38 + 19 + 33

It can be written as

= 38 – 32 – 26 – 28 + 33 – 26 + 19

So we get

= 6 – 26 – 28 + 7 + 19

By calculation

= 6 – 28 – 26 + 26

= 6 – 28

By subtraction

= – 22

(ii) – 26 – 20 + 33 – (-33) + 21 + 24 – (-25) – 26 – 14 – 34

We get

= – 46 + 33 + 33 + 21 + 24 + 25 – 26 – 14 – 34

On further calculation

= – 46 + 66 + 21 + 24 + 25 + (-74)

It can be written as

= – 46 + 66 + 70 – 74

So we get

= – 46 – 4 + 66

By calculation

= – 50 + 66

= 66 – 50

By subtraction

= 16

9. Calculate

1 – 2 + 3 – 4 + 5 – 6 + ……… + 15 – 16

Solution:

It can be written as

1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + 9 – 10 + 11 – 12 + 13 – 14 + 15 – 16

We get

= – 1 – 1 – 1 – 1 – 1 – 1 – 1 – 1

By calculation

= – 8

10. Calculate the sum:

5 + (-5) + 5 + (-5) + …..

(i) if the number of terms is 10.

(ii) if the number of terms is 11.

Solution:

(i) if the number of terms is 10

We get

5 + (-5) + 5 + (-5) + 5 + (-5) + 5 + (-5) + 5 + (-5)

On further calculation

= 5 – 5 + 5 – 5 + 5 – 5 + 5 – 5 + 5 – 5 = 0

(ii) if the number of terms is 11

We get

5 + (-5) + 5 + (-5) + 5 + (-5) + 5 + (-5) + 5 + (-5) + 5

On further calculation

= 5 – 5 + 5 – 5 + 5 – 5 + 5 – 5 + 5 – 5 + 5 = 5

11. Replace * by < or > in each of the following to make the statement true:

(i) (-6) + (-9) * (-6) – (-9)

(ii) (-12) – (-12) * (-12) + (-12)

(iii) (-20) – (-20) * 20 – (65)

(iv) 28 – (-10) * (-16) – (-76)

Solution:

(i) (-6) + (-9) < (-6) – (-9)

(ii) (-12) – (-12) > (-12) + (-12)

(iii) (-20) – (-20) > 20 – (65)

(iv) 28 – (-10) < (-16) – (-76)

12. If △ is an operation on integers such that a △ b = – a + b – (-2) for all integers a, b. Find the value of

(i) 4 △ 3

(ii) (-2) △ (-3)

(iii) 6 △ (-5)

(iv) (-5) △ 6

Solution:

(i) 4 △ 3

By substituting values in a △ b = – a + b – (-2)

We get

4 △ 3 = – 4 + 3 – (-2) = 1

(ii) (-2) △ (-3)

By substituting values in a △ b = – a + b – (-2)

We get

(-2) △ (-3) = – (-2) + (-3) – (-2) = 1

(iii) 6 △ (-5)

By substituting values in a △ b = – a + b – (-2)

We get

6 △ (-5) = – 6 + (-5) – (-2) = – 9

(iv) (-5) △ 6

By substituting values in a △ b = – a + b – (-2)

We get

(-5) △ 6 = – (-5) + 6 – (-2) = 13

13. If a and b are two integers such that a is the predecessor of b. Find the value of a – b.

Solution:

It is given that a is the predecessor of b

We can write it as

a + 1 = b

So we get

a – b = – 1

14. If a and b are two integers such that a is the successor of b. Find the value of a – b.

Solution:

It is given that a is the successor of b

We can write it as

a – 1 = b

So we get

a – b = 1

15. Which of the following statements are true:

(i) – 13 > – 8 – (-2)

(ii) – 4 + (-2) < 2

(iii) The negative of a negative integer is positive.

(iv) If a and b are two integers such that a > b, then a – b is always a positive integer.

(v) The difference of two integers is an integer.

(vi) Additive inverse of a negative integer is negative.

(vii) Additive inverse of a positive integer is negative.

(viii) Additive inverse of a negative integer is positive.

Solution:

(i) False.

(ii) True.

(iii) True.

(iv) True.

(v) True.

(vi) False.

(vii) True.

(viii) True.

16. Fill in the blanks:

(i) – 7 + ….. = 0

(ii) 29 + ….. = 0

(iii) 132 + (-132) = ….

(iv) – 14 + ….. = 22

(v) – 1256 + ….. = – 742

(vi) ….. – 1234 = – 4539

Solution:

(i) – 7 + 7 = 0

(ii) 29 + (-29) = 0

(iii) 132 + (-132) = 0

(iv) – 14 + 36 = 22

(v) – 1256 + 514 = – 742

(vi) -3305 – 1234 = – 4539

Objective Type Questions page: 5.18

Mark the correct alternative in each of the following:

1. Which of the following statement is true?
(a) − 7 > − 5              (b) − 7 < − 5                 (c) (− 7) + (− 5) > 0                       (d) (− 7) − (− 5) > 0

Solution:

The option (b) is correct answer.

In option (a)

We know that − 7 is to the left of – 5

Hence, − 7 < − 5.

In option (c)

We know that (− 7) + (− 5) = − (7 + 5) = − 12.

So − 12 is to the left of 0

Hence (− 7) + (− 5) < 0.

In option (d)

(− 7) − (− 5) = (− 7) + (additive inverse of − 5) = (− 7) + (5) = − (7 − 5) = − 2

We know that − 2 is to the left of 0, so (− 7) − (− 5) < 0.

2. 5 less than − 2 is
(a) 3                            (b) − 3                        (c) − 7                                 (d) 7

Solution:

The option (c) is correct answer.

We know that, 5 less than − 2 = (− 2) − (5) = − 2 − 5 = − 7

3. 6 more than − 7 is
(a) 1                            (b) − 1                        (c) 13                                 (d) – 13

Solution:

The option (b) is correct answer.

We know that, 6 more than − 7 = (− 7) + 6 = − (7 − 6) = − 1

4. If x is a positive integer, then
(a) x + |x| = 0              (b) x − |x| = 0                    (c) x + |x| = −2x                (d) x = − |x|

Solution:

The option (b) is correct answer.

We know that if x is positive integer, then |x| = x

Hence, x + |x| = x + x = 2x and x − |x| = x − x = 0

5. If x is a negative integer, then
(a) x + |x| = 0              (b) x − |x| = 0                    (c) x + |x| = 2x                (d) x − |x| = − 2x

Solution:

The option (a) is correct answer.

We know that x is negative integer, then |x| = −x

It can be written as

x + |x| = x − x = 0 and x − |x| = x − (− x) = x + x = 2x

6. If x is greater than 2, then |2 − x| =
(a) 2 − x              (b) x − 2                    (c) 2 + x                (d) − x – 2

Solution:

The option (b) is correct answer.

We know that if a is negative integer, then |a| = − a

It is given that x is greater than 2 where 2 − x is negative

Hence, |2 − x| = − (2 − x) = − 2 + x = x − 2.

7. 9 + |− 4| is equal to
(a) 5                         (b) − 5                       (c) 13                            (d) −13

Solution:

The option (c) is correct answer.

We know that, |− 4| = 4

Hence 9 + |− 4| = 9 + 4 = 13

8. (− 35) + (− 32) is equal to
(a) 67                         (b) − 67                       (c) − 3                            (d) 3

Solution:

The option (b) is correct answer.

It can be written as (− 35) + (− 32) = − (35 + 32) = − 67

9. (− 29) + 5 is equal to
(a) 24                         (b) 34                       (c) − 34                            (d) – 24

Solution:

The option (d) is correct answer.

It can be written as (− 29) + 5 = − (29 − 5) = − 24

10. |− |− 7| − 3| is equal to
(a) − 7                       (b) 7                              (c) 10                                    (d) – 10

Solution:

The option (c) is correct answer.

It can be written as |− |− 7| − 3| = |− 7 − 3| = |− 10| = 10                                         

11. The successor of − 22 is
(a) − 23                       (b) − 21                              (c) 23                                    (d) 21

Solution:

The option (b) is correct answer.

We know that if ‘a’ is an integer a + 1 is its successor.

So the successor of − 22 = − 22 + 1 = − (22 − 1) = − 21

12. The predecessor of – 14 is

(a) – 15 (b) 15 (c) 13 (d) – 13

Solution:

The option (a) is correct answer.

The predecessor of – 14 is – 15.

13. If the sum of two integers is − 26 and one of them is 14, then the other integer is
(a) − 12                       (b) 12                              (c) − 40                               (d) 40

Solution:

The option (c) is correct answer.

It is given that the sum of two integers = − 26

One of them = 14

So the other integer = − 26 − 14 = − (26 + 14) = − 40

14. Which of the following pairs of integers have 5 as a difference?
(a) 10, 5                       (b) − 10, − 5                          (c) 15, − 20                               (d) both (a) and (b)

Solution:

The option (d) is correct answer.

Consider option (a) 10 − 5 = 5

Consider option (b) (− 5) − (− 10) = − 5 + 10 = 5

Consider option (c) 15 − (− 20) = 15 + 20 = 35

15. If the product of two integers is 72 and one of them is − 9, then the other integers is
(a) − 8                       (b) 8                          (c) 81                               (d) 63

Solution:

The option (a) is correct answer.

It is given that the product of two integers = 72

One of them = − 9

Hence, the other integers = 72 ÷ (− 9) = − 8

16. On subtracting − 7 from − 14, we get
(a) − 12                       (b) − 7                          (c) −14                               (d) 21

Solution:

The option (b) is correct answer.

It can be written as

Required number = − 14 − (− 7) = − 14 + 7 = − (14 − 7) = − 7

17. The largest number that divides 64 and 72 and leave the remainders 12 and 7 respectively, is
(a) 17                             (b) 13                                       (c) 14                                      (d) 18

Solution:

The option (b) is correct answer.

By subtracting 12 and 7 from 64 and 72

We get

64 − 12 = 52 and 72 − 7 = 65

So the required number is the HCF of 52 and 65.

It can be written as

52 = 4 × 13 and 65 = 5 × 13

HCF 52 and 65 = 13

Hence, the largest number that divides 64 and 72 and leave the remainder 12 and 7 respectively, is 13.

18. The sum of two integers is − 23. If one of them is 18, then the other is
(a) −14                             (b) 14                                    (c) 41                                    (d) −41

Solution:

The option (d) is correct answer.

It is given as the sum of integers = − 23

One of them = 18

So the other number = (− 23) − (18) = − 23 − 18 = − (23 + 18) = − 41

Hence, the other number is − 41.

19. The sum of two integers is − 35. If one of them is 40, then the other is
(a) 5                             (b) − 75                                    (c) 75                                    (d) – 5

Solution:

The option (b) is correct answer.

It is given that the sum of integers = − 35

One of them = 40

So the other number = (− 35) − (40) = − 35 − 40 = − (35 + 40) = − 75

Hence, the other number is − 75.

20. On subtracting − 5 from 0, we get
(a) − 5                             (b) 5                                    (c) 50                                    (d) 0

Solution:

The option (d) is correct answer.

We know that, 0 − (− 5) = 0 + 5 = 5

Hence by subtracting − 5 from 0, we obtain 5.

21. (− 16) + 14 − (− 13) is equal to
(a) − 11                             (b) 12                                    (c) 11                                    (d) – 15

Solution:

The option (c) is correct answer.

It can be written as (− 16) + 14 − (− 13) = (− 16) + 14 + 13 = (− 16) + 27 = 27 − 16 = 11

22. (− 2) × (− 3) × 6 × (− 1) is equal to
(a) 36                             (b) − 36                                (c) 6                                    (d) – 6

Solution:

The option (b) is correct answer.

It can be written as (− 2) × (− 3) × 6 × (− 1) = (2 × 3) × 6 × (− 1) = 6 × 6 × (− 1) = 36 × (− 1)

So we get (− 2) × (− 3) × 6 × (− 1) = − (36 × 1) = − 36

23. 86 + (- 28) + 12 + (- 34) is equal to
(a) 36                             (b) − 36                                (c) 6                                    (d) – 6

Solution:

The option (c) is correct answer.

It can be written as 86 + (−28) + 12 + (−34) = 86 + (−28) − (34 − 12) = 86 + (−28) − 22

On further calculation

86 + (−28) + 12 + (−34) = (86 − 28) − (34 − 12) = 58 − 22 = 36

24. (−12) × (−9) − 6 × (−8) is equal to
(a) 156                             (b) 60                                (c) −156                                    (d) – 60

Solution:

The option (a) is correct answer.

It can be written as (−12) × (−9) − 6 × (−8) = (12 × 9) − 6 × (−8) = 108 − 6 × (−8) 

On further calculation

86 + (−28) + 12 + (−34) = 108 + 6 × 8 = 108 + 48 = 156